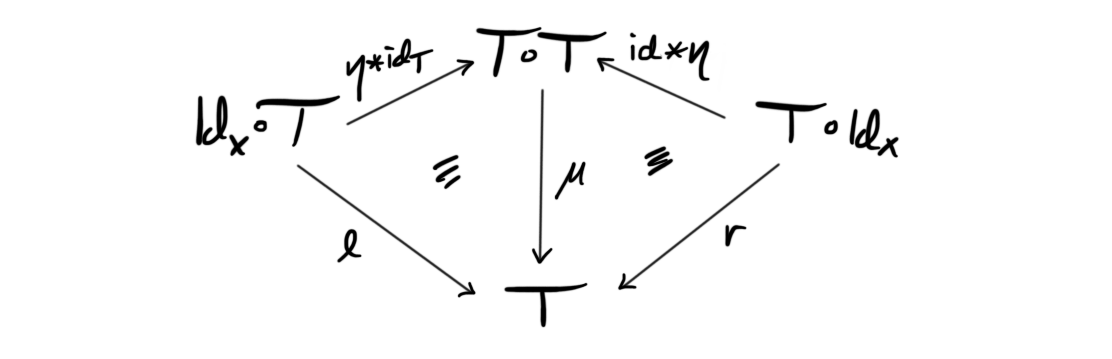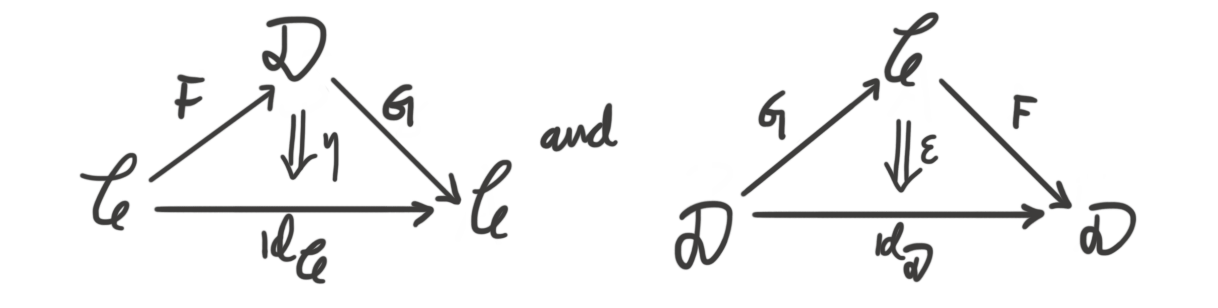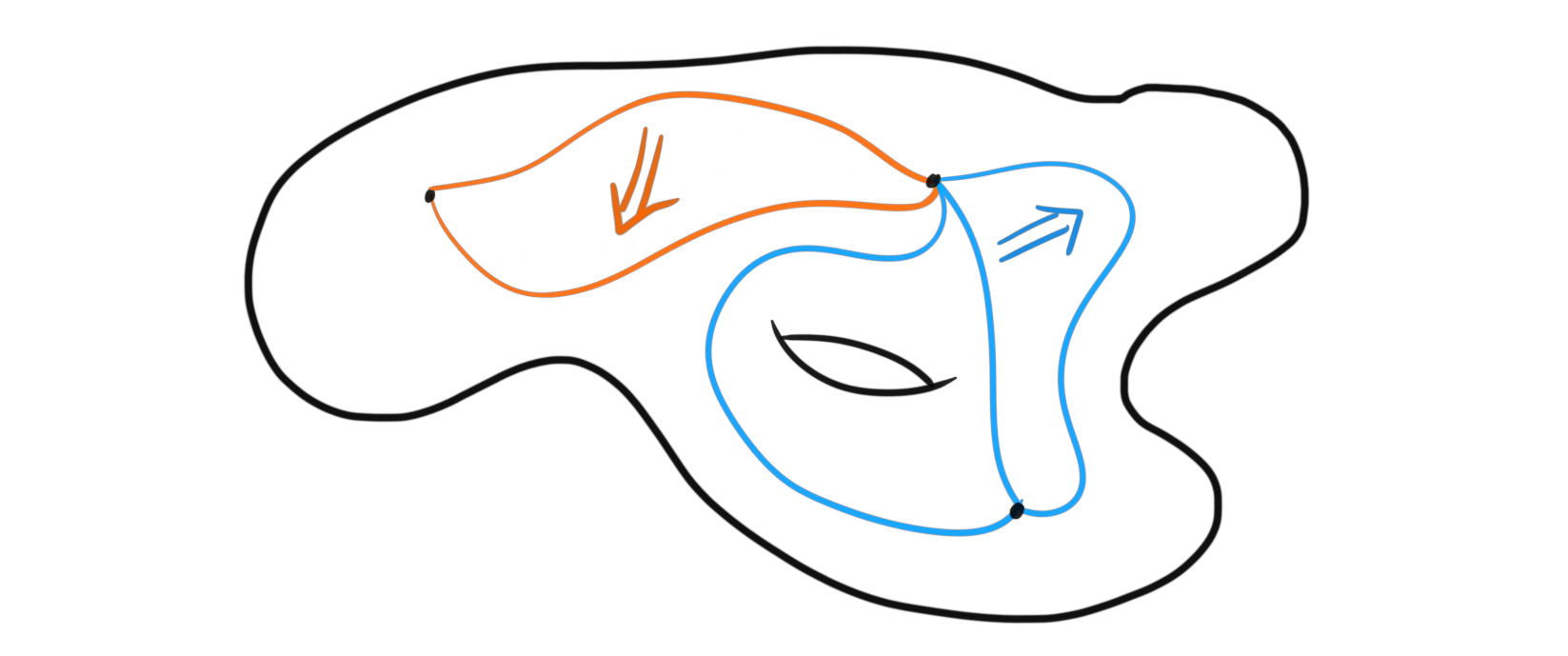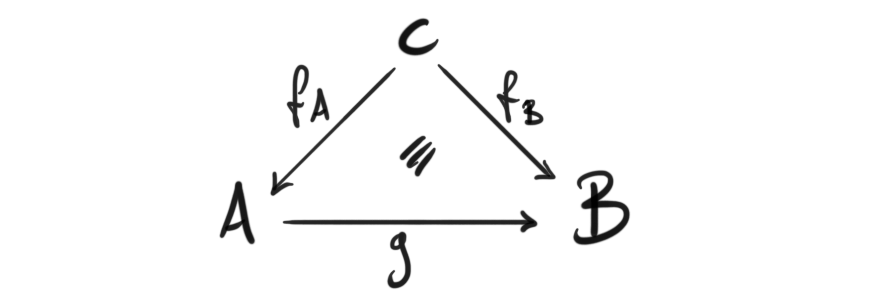
Quasi-categories
A couple weeks ago I held a talk on introductory higher category theory. Most of the talk was based upon thing we already have discussed on this blog, such as the strict $2$-category $Cat$, bicategories, and why strictness fails for the category of topological spaces. The inly thing I talked about which I haven’t yet featured on this blog is the notion of quasi-categories, so I though that I would do that today....