I think there are many parts of physics worth studying for mathematicians, and the physical notion of a cosmos may be one of them, but, this post is not about physics. Even though the usual field of study one thinks of when hearing the word “cosmos” is physics, there is also a type of mathematical object with the same name. This type of object does have that name for a reason, which is not clear maybe from the object it self, but from what one can do with and in such an object. In physics, the cosmos is a word for the universe, but it includes also the universes structure. The cosmos is not just “all the stuff that exists”, but also their relations and complex interactions. It is therefore kind of the background, or the playing field of physics.
A cosmos in mathematics is also a kind of nice playing field for mathematics. More specifically ncatlab says it is “a nice place to do category theory”. But what does this mean? Well, it is kind of complicated, but we will try to understand some of it. To be more precise without explaining anything more, one could say the idea is that the theory of categories enriched over a cosmos behave similarly to standard category theory itself. Much of this theory is still way above my head, so Ill try to keep it grounded. That said, we need to understand what an enriched category is to tell the story of the cosmos properly. This is the goal for this post, and next time we will come back to looking at what properties a cosmos should have for our above statement to be true. Throughout we will try our best to pretend that the definition is motivated by physics.
More structure
Often when doing category theory or homological algebra we often find that we need some restrictions on our category to make it nicer to work with, or to have more nice properties. First of all we often note that it is usually enough to work in locally small categories, i.e. categories where the collection of morphisms between two objects always form a set. Many authors even require this for their definition of a category. Sets in themselves are not always exciting enough, so we often require that these sets of morphisms have some structure, often an algebraic one. This is intuitively exactly what an enriched category is, i.e. some category where all sets of morphisms are actually objects in some other fixed category, i.e. we have objects of morphisms. Hence we can talk about categories “enriched over” another category, or sometimes authors use “enriched in” instead.
We see quite quickly that the category from where we steal our objects of morphisms needs to have at least one property. In a category we need to be able to compose morphisms, and when these morphisms come from an object, their composition also must come from an object, and hence we need some way to take the product of objects. This is formalized by the category being a monoidal category, i.e. a category where we have some sort of product that behave nicely. This is easier said than done, and the following long definition reflects that.
Definition (Monoidal category): A monoidal category is a category $\mathcal{C}$ equipped with a functor $\otimes : \mathcal{C} \times \mathcal{C} \rightarrow \mathcal{C},$ called the monoidal product, a unit object $1\in \mathcal{C}$ and three natural isomorphisms $\lambda_A : 1\otimes A \rightarrow A$, $\rho_A : A\otimes 1\rightarrow A$ and $\alpha_{A,B,C} : (A\otimes B)\otimes C \rightarrow A\otimes (B\otimes C)$ called the left unitor, right unitor and associator respectively, such that the following diagrams
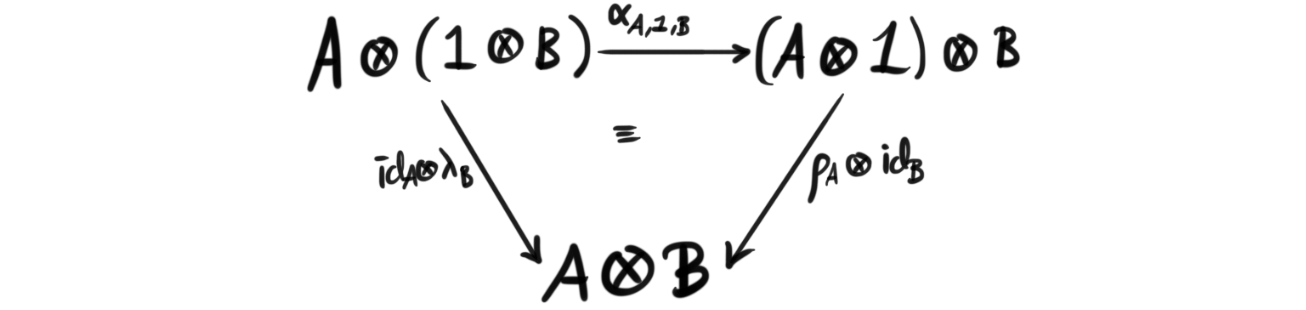
called the triangle identity, and
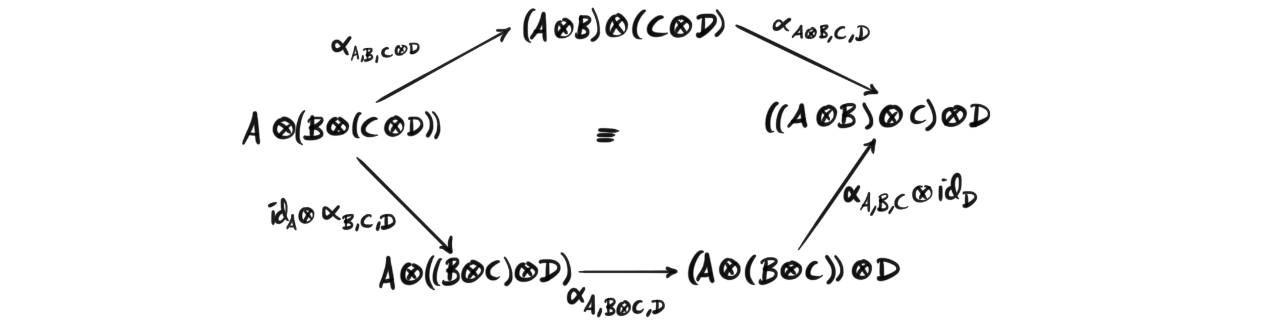
called the pentagon identity, both commute.
The definition seems very difficult, and has a lot of moving parts, but in reality it is quite simple. We are using the symbol for the tensor product, $\otimes$ for the monoidal product because the tensor product is usually the product we are using. So any intuition we have from using the tensor product can usually be applied to monoidal categories. If the three natural isomorphisms $\lambda, \rho, \alpha$ are identities, then $\mathcal{C}$ is called a strict monoidal category. These do rarely come up in nature, but every monoidal category is in fact equivalent to a strict monoidal category.
A version of the monoidal category we will be using is actually a bit nicer, and comes with an extra bit of information, namely symmetry.
Definition (Symmetric monoidal category): Let $\mathcal{C}$ be a monoidal category. We say $\mathcal{C}$ is a symmetric monoidal category if there is a natural isomorphism $\beta_{X,Y}: X\otimes Y \rightarrow Y \otimes X$, called the braid isomorphism, such that $\beta_{X,Y}\circ \beta_{Y,X} = id_{X\otimes Y}$ and the following diagrams
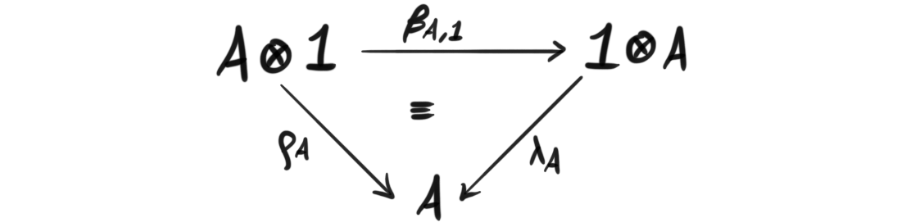
called the unit coherence, and
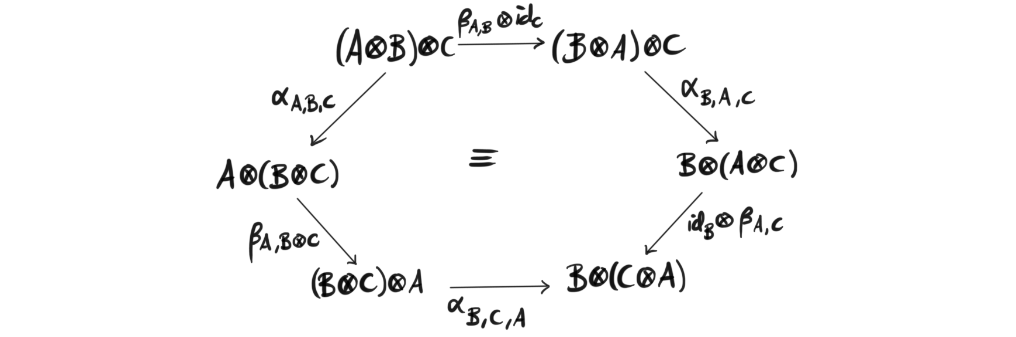
called the associativity coherence, both commute.
Just to mention it, there is a version of this type of category where we relax the definition a bit, such that the composition $\beta_{X,Y}\circ \beta_{Y,X}$ is not the identity. This is then called a braided monoidal category, and is often used in knot theory.
To have some quick examples, most categories that appear in the wild are symmetric monoidal. For example the category of sets with the regular cartesian product is symmetric monoidal, the category of groups with the cartesian product is symmetric monoidal, and the category of finite dimensional vector spaces with the tensor product is symmetric monoidal.
Enriched categories
So, with that definition under our belt, we are ready to tackle the next definition, which is really what we want to understand, namely enriched categories.
Definition (Enriched category): Let $\mathcal{V}$ be a monoidal category. A $\mathcal{V}$-category $\mathcal{C}$, or a category enriched over $\mathcal{V}$, consists of a collection of objects, denoted $Ob\mathcal{C}$, and for every pair $A,B$ of objects in $\mathcal{C}$ we have an object $C(A,B) \in \mathcal{V}$, called the hom object, or the object of morphisms. These collections must satisfy that for any object $A$ in $\mathcal{C}$ there is a morphism $j_A : 1\rightarrow C(A,A)$ called the identity element, and for every triple of objects $A, B, C$ in $\mathcal{C}$ there is a morphism $\circ_{A,B,C}: C(B,C)\otimes C(A,B)\rightarrow C(A,C)$ called composition such that the following three diagrams commute.
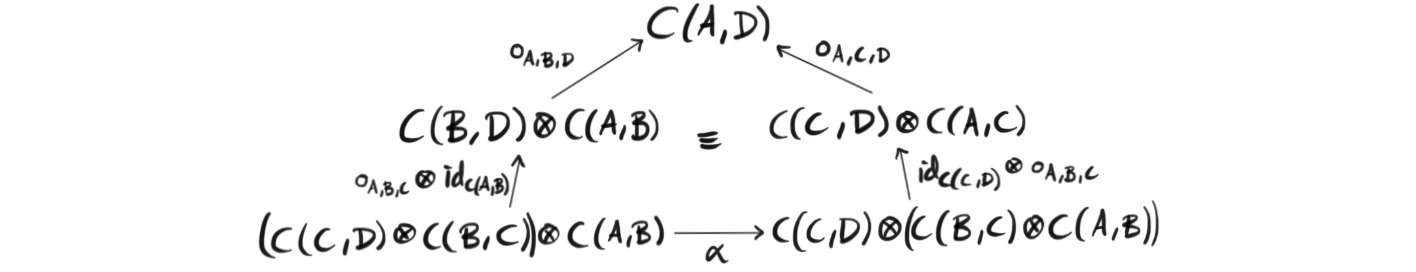
Which expresses the associativity of composition,
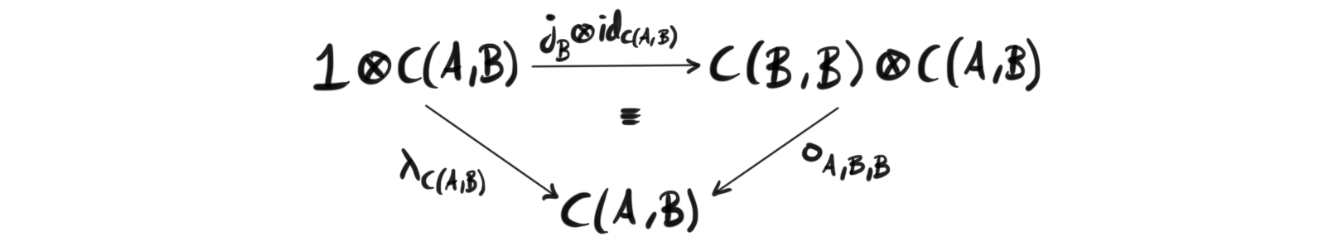
and
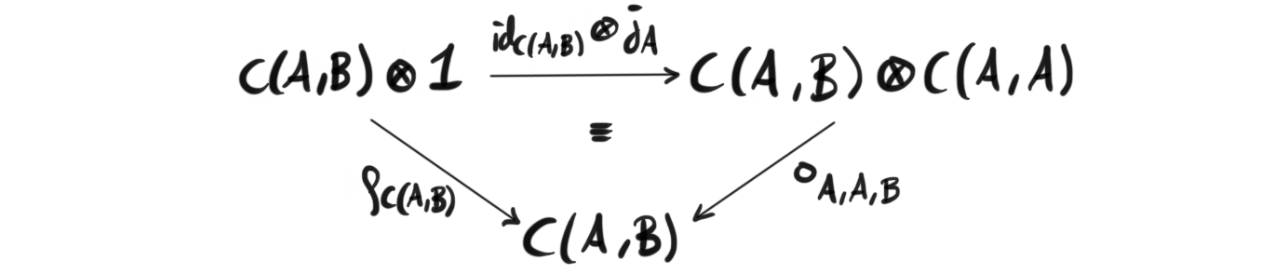
where the latter two replace our standard notion of identity morphism with a more appropriate one when using the identity object 1 from our monoidal category $\mathcal{V}$.
We see that our intuitive notion of an enriched category took quite a long time to explain, and had a lot of bits and pieces that needs to be correct. But, our intuitive explanation, i.e. a category where we have objects of morphisms instead of just collections of morphisms is still the nice way of thinking about these abstract complicated mathematical structures. To have a couple examples, we first look at the part we mentioned in the introduction, that we usually require our category to be locally small. Here our potential class of morphisms that usually define a category is required to be sets. So, we have taken sets, which form a monoidal category $Set$ under the cartesian product, and stolen them for our hom objects, i.e. a locally small category is just a $Set$-category, or a category enriched in Set. This is the first stepping stone to realizing that maybe enriched categories are nice to work with after all!
If we want some algebraic structures on these sets, we can instead enrich our category over the category of abelian groups, which is monoidal under the tensor product when viewing them as $\mathbb{Z}$-modules. These categories are the pre-additive categories. Familiar examples such as the category of abelian groups, the category of modules over a commutative ring and the category of vector spaces are actually all enriched over themselves, as their morphisms all form objects in the category. There are of course some more wacky examples, such as viewing a generalized type of metric space as a category enriched over the poset $([0,\infty], \geq)$ of extended real numbers, where the monoidal product is just standard addition. An example related to this is a recent paper by (among others) of one of my favorite math-bloggers Math3ma, which used a similar idea to try to understand language as a category enriched over the unit interval with multiplication as the monoidal product. She and her collaborator did this by having the hom-objects be the conditional probability $p(s'|s)$ that $s$ is a subsequence of the sequence $s'$, and use this to understand something which I didn’t understand.
As you can tell, the possibilities, and the examples are many and diverse. But we are not merely interested in these enriched categories. We are interested in which objects it is nice to enrich over. This will be done in part 2 of this mini series, where we explore the remaining pieces to defining a cosmos, and at the end hopefully define it in all its glory. To hint a bit at where we are heading, we want to define $\mathcal{V}-Cat$ of categories enriched over $\mathcal{V}$, and that this category behaves like a standard category, i.e. we have nice morphisms, natural transformations, a Yoneda lemma, equivalences and adjunctions etc. We will not prove that all of these have an enriched version, but interested readers can study “Basic concepts of enriched category theory” by G.M. Kelly.