A couple weeks ago I held a talk on introductory higher category theory. Most of the talk was based upon thing we already have discussed on this blog, such as the strict $2$-category $Cat$, bicategories, and why strictness fails for the category of topological spaces. The inly thing I talked about which I haven’t yet featured on this blog is the notion of quasi-categories, so I though that I would do that today. So, to see where we are headed, I just define it right away.
Definition (quasi-category): A quasi-category is a simplicial set where every inner horn has a filler.
This definition is incredibly short and sweet, but packs a serious punch once we unravel it. It is also often stated as a quasi-category being a simplicial set satisfying the weak Kan condition. There are many ways to intuitively justify the existence of quasi-categories, and one of them we almost already know. We have previously discussed $\infty$-groupoids as just topological spaces through the homotopy hypothesis. From Quillen we know that the homotopy theory of topological spaces and the homotopy theory of simplicial sets are equivalent. More precisely, the category of topological spaces is Quillen equivalent to the category of simplicial sets. Instead of $\infty$-groupoids—which are $(\infty, 0)$-categories as every morphism of every degree is invertible up to a coherent homotopy—we can talk about $(\infty, 1)$-categories. These are intuitively a collection of objects and morphisms such that all homsets are $\infty$-groupoids. The most classical example being just the category of topological spaces, or more generally categories enriched in topological spaces, often called topological categories. Now we maybe start to see an idea of why quasi-categories are defined through simplicial sets. We can pass over to categories enriched in simplicial spaces, which gets us a bit closer to the definition, but not quite.
I want to remark that the above section is only for broad intuition, and that I’m both shoving an incredible load of details under the rug, and lack a solid understanding of the technicalities. But, for me at least, it gives a picture of why we care about introducing simplicial sets into higher category theory, without going through the whole nerve of a category business.
Simplicial sets
Time to start unraveling the definition. I said a quasi-category was a simplicial set, so this is probably a good place to start. To define a simplicial set we first need to define the simplex category $\Delta$.
Definition (the simplex category): The simplex category $\Delta$ is the category consisting of all finite totally ordered sets with (non-strict) order preserving maps. We write the objects as $[n] = {0,1,2,3, \ldots}$.
The category $\Delta$ is generated by two important classes of maps, called the face maps and the degeneracy maps. The $i$‘th face map $\delta_n^i$ is defined as the unique order preserving injection $\delta_n^i: [n-1]\longrightarrow [n]$ that misses $i$ and the $i$‘th degeneracy map $\sigma_n^i$ is defined as the unique surjection $\sigma_n^i:[n]\longrightarrow [n-1]$ that hits $i$ twice.
Definition (simplicial set): A simplicial set is a functor $X: \Delta^{op} \longrightarrow Set$. We write $X_n = X([n])$ and call it the $n$-simplicies of $X$.
These again form a category, $sSet$ where the morphisms are the natural transformations between the simplicial sets.
The most important examples of simplicial sets are the so-called standard $n$-simplexes $\Delta^n$. These are defined to be $\Delta^n = Hom([n], -)$, where the functor $Hom([n], – )$ is on the opposite category, so we can use it as $Hom(-, [n])$ on the normal simplex category. These standard simplexes are the simplest ones to think about and the simplest to visualize. This is because we can apply the geometric realization functor, and these become the familiar $n$-simplexes we use in topology! Hence we can think of for example $\Delta^3$ as
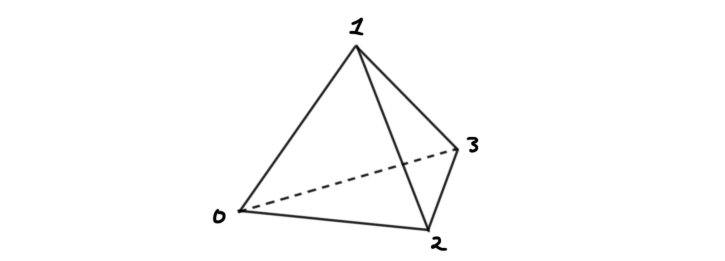
Due to the Yoneda lemma, the $n$-simplicies of a simplicial set $X$ are in one to one correspondence with maps $\Delta^n \longrightarrow X$ in the category of simplicial sets.
We have now covered what a quasi-category consists of, namely a simplicial set. So, next we need to understand the condition we put on that simplicial set.
Horns and fillers
The condition we asked for included another simplicial set we need to define, namely the the simplicial $k$-horns. These are very similar to the standard simplices, but are missing one of the sides. To be rigorous we define the $i$‘th side of $\delta^n$ to be the image of $\Delta^{n-1}$ under the inclusion $\iota_i$ onto the side of $\Delta^n$ opposite to $i$. The $0$‘th side of $\Delta^3$ under the geometric realization functor would then be the orange side in the following picture.

We then use these sides to construct what we call simplicial horns.
Definition (The simplicial k-horn): The simplicial $k$-horn is the union of all sides of $\Delta^n$ except the $k$‘th one, i.e.
$$\Lambda_k^n = \bigcup_{i\neq k} Im(\iota_i:\Delta^{n-1}\longrightarrow \Delta^n). $$
A $k$-horn in a simplicial set $X$ is then a map $\Lambda_k^n \longrightarrow X$. We call it an inner horn if $0<k<n$.
We wanted these $k$-horns in our simplicial set to satisfy a condition, which we called the weak Kan condition. This condition tells us that certain lifts of maps related to the $k$-horns in a simplicial set $X$ exists. We have a canonical inclusion from the simplicial $k$-horn into $\Delta^n$ and we want there to exist a lift through this map for every inner horn in $X$, i.e. that the dotted map exists
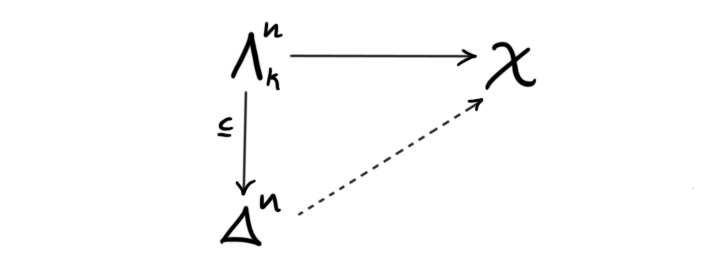
If such a lift exists for all inner horns in a simplicial set $X$ we say it satisfies the weak Kan condition. We have now unrolled the definition, and we can state it with a bit more insight.
Definition (quasi-category): A quasi-category is a simplicial set $X$ such that every horn $\Lambda_k^n \longrightarrow X$ lifts to a map $\Delta^n\longrightarrow X$ through the canonical inclusion $\Lambda_k^n\subset \Delta^n$.
So what does this definition really mean? What does this even have to do with categories? The connecting piece is interpreting horns as composable morphisms in a category. The easiest to visualize is the lift of the horn $\Lambda_1^2$. If we draw it it looks like
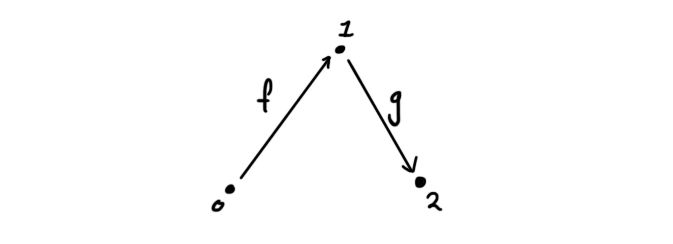
and an existing lift means there exists a dotted map
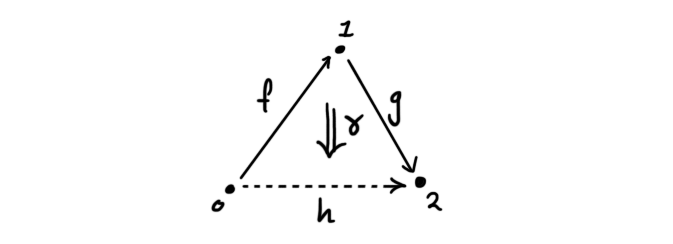
making the triangle commute up to a higher morphism. In other words, we have some weaker form of composition of composable morphisms in the quasi-category. There may be many different ways to compose the morphisms, to we can’t talk about “the” composition, but all of the different compositions are related by higher morphisms. In this way we can view a quasi-category as a weaker notion of category, where we have morphisms that compose non-uniquely, and have an infinite tower of morphisms between morphisms to relate the compositions and higher relations. If we insist that the lift in the weak Kan condition is unique, we actually have an object we can use as a definition for a category, hence quasi-categories generalize categories, which is what we wanted, and justifies the word “quasi” being put in front.
That was all I wanted to say today, but we will definitely revisit quasi-categories later as the theory built by Lurie and Joyal around these objects are too interesting to not look deeper into!