Welcome to my mathematics blog. On here I write my way through my mathematical endevours, mostly focusing on algebraic topology, but also other things that interests me.

Exotic algebraic models
This blog-post is dedicated to this day, $\pi$-day (14th of march), where we celebrate $\pi_*$, the stable homotopy groups. As has been the case a couple of times already, when faced with an increased workload I tend to neglect writing on this blog. It is only natural that increased amounts of work in one section lead to a decreased amount of work in another — there is, after all, only a finite amount of time given to us....

Hopf algebroids
Introduction In the last blog post we introduced and studied adapted homology theories. Given a stable $\infty$-category $\mathcal{C}$ and $\mathcal{A}$ an abelian category with enough injectives together with a local grading $[1]\colon \mathcal{A}\longrightarrow \mathcal{A}$, an adapted homology theory is a functor $$ H\colon \mathcal{C}\longrightarrow \mathcal{A} $$ such that $H$ is additive, sends fiber sequences to long exact sequences, sends the suspension $\Sigma$ of $\mathcal{C}$ to the shift $[1]$ of $\mathcal{A}$ and such that we can lift injectives in $\mathcal{A}$ into $\mathcal{C}$ through $H$....

Adapted homology
Introduction In the last post we studied homology theories as abstract functors from stable $\infty$-categories to abelian categories. We showed that for every stable $\infty$-category $\mathcal{C}$ there is a universal homology theory which all others factor through, namely the Yoneda embedding into the Freyd envelope, $$ y\colon \mathcal{C}\longrightarrow A(\mathcal{C}). $$ The fact that this is universal means that for any homology theory $H\colon \mathcal{C}\longrightarrow \mathcal{A}$ there is an essentially unique factorization...

Universal homology
New year; same me; new math. During the fall I said that I wanted to post on this blog monthly, but that did not happen for some reason. I thought I’d try again this semester, but maybe I am setting this not that high bar still too high for my self. For some reason there seems to be fewer hours in the day than it used to. The cover page for the post is generated by Dalle·2 using the prompt “A man finding the universal piece, old painting” – a true work of art....

Chromatic redshift
In a recent lunch conversation with Nils Baas we, among a plethora of other things, discussed the chromatic redshift phenomenon in stable homotopy theory. Nils was explaining some things about the results he had published together with Bjørn Dundas and John Rognes on using $2$-vector bundles to explain the algebraic K-theory of topological K-theory, i.e. $K(ku)$. This spectrum has height $2$, and since $ku$ has height $1$ this exhibits a phenomenon called redshift....

Periodic torsion is torsion periodic
Hi, long time no see. I used to be very persistent about writing at least one blog-post each month, but as one can see, I have taken a break for a couple months due to vacation and increased teaching and lecturing duties at NTNU. Incidentally it coincided exactly with the 2 year mark of having posted at least once a month, often more. I have been writing stuff, but not anything worth posting....

Johnson-Wilson theory
It has been some time since we studied at the correlation between formal group laws, which were certain power series that looked like Taylor expansion of multiplication on a Lie group, and complex oriented cohomology theories. In particular, we learned that these two completely separate notions had a common universal object. The universal formal group law over the Lazard ring was the same as the formal group law determined by the universal complex oriented cohomology theory — complex cobordism cohomology....
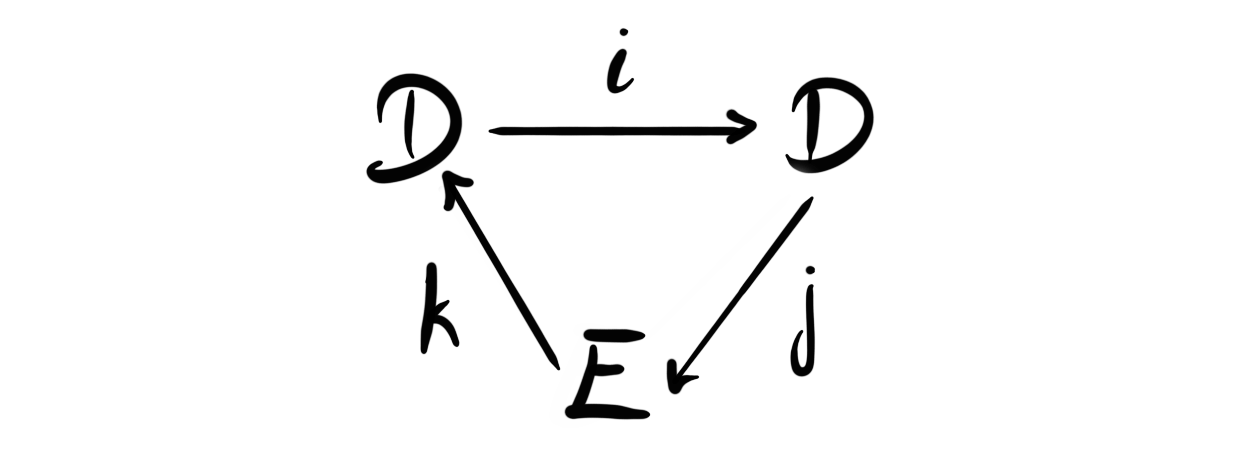
Stable infinity-categories
This semester I am taking part in a seminar on $\infty$-categories, administered by Rune Haugseng. So far we have covered roughly: the basic definitions, fibrations, limits, colimits, Joyal’s lifting theorem, equivalences, straightening, Yoneda lemma, adjunctions and Kan extensions. This week it is my turn to give a talk on stable $\infty$-categories, and this blog post will hopefully be some sort of lecture notes for this talk. The intersection of things in this post and the contents of the talk should at least be non-empty....
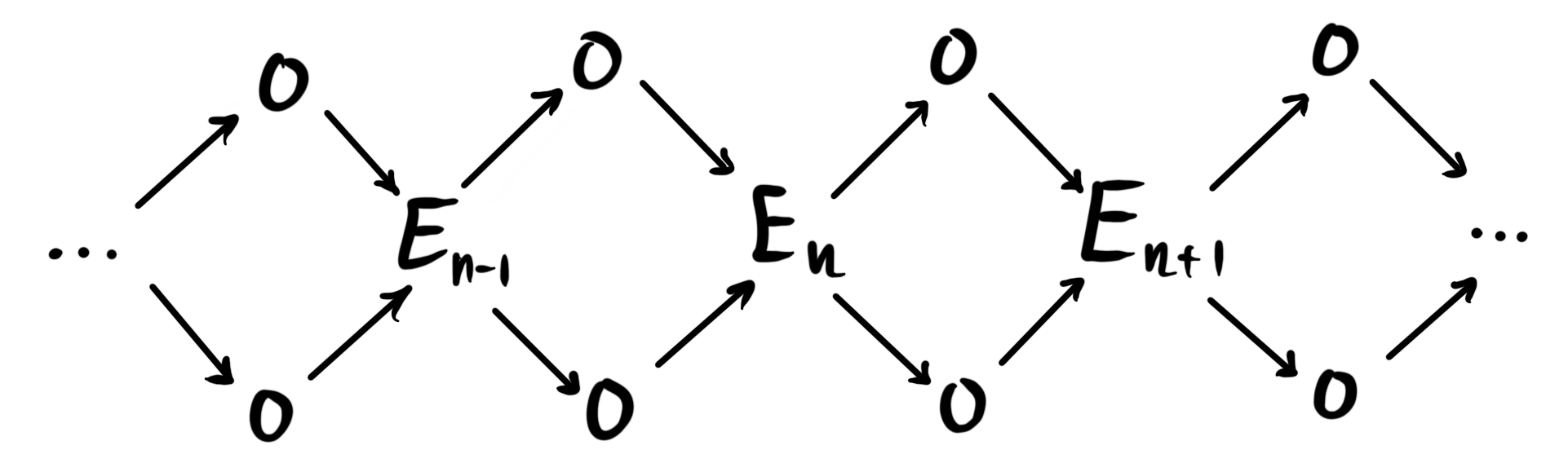
The Adams spectral sequence
Recently my friend Elias started his own math blog adventure, and his first post gave a nice introduction to spectral sequences. Reading it I remembered that I should really understand some of the parts better myself, because a lot of the arguments one makes in chromatic homotopy theory are based on spectral sequences. There is a framework for constructing spectral sequences that are not covered in my old post on them, as well as Elias’ post, and that is creating spectral sequences from exact couples....
Brown-Peterson cohomology
Over the holidays sadly Edgar H. Brown passed away. He was one of the influential men behind many of the concepts this blog has featured and will feature in the future. This post is in particular focused on one of these concepts, namely Brown-Peterson cohomology and the Brown-Peterson spectrum. In the last post we developed the category of $p$-local spectra, and in the post before that we explored complex cobordism cohomology....