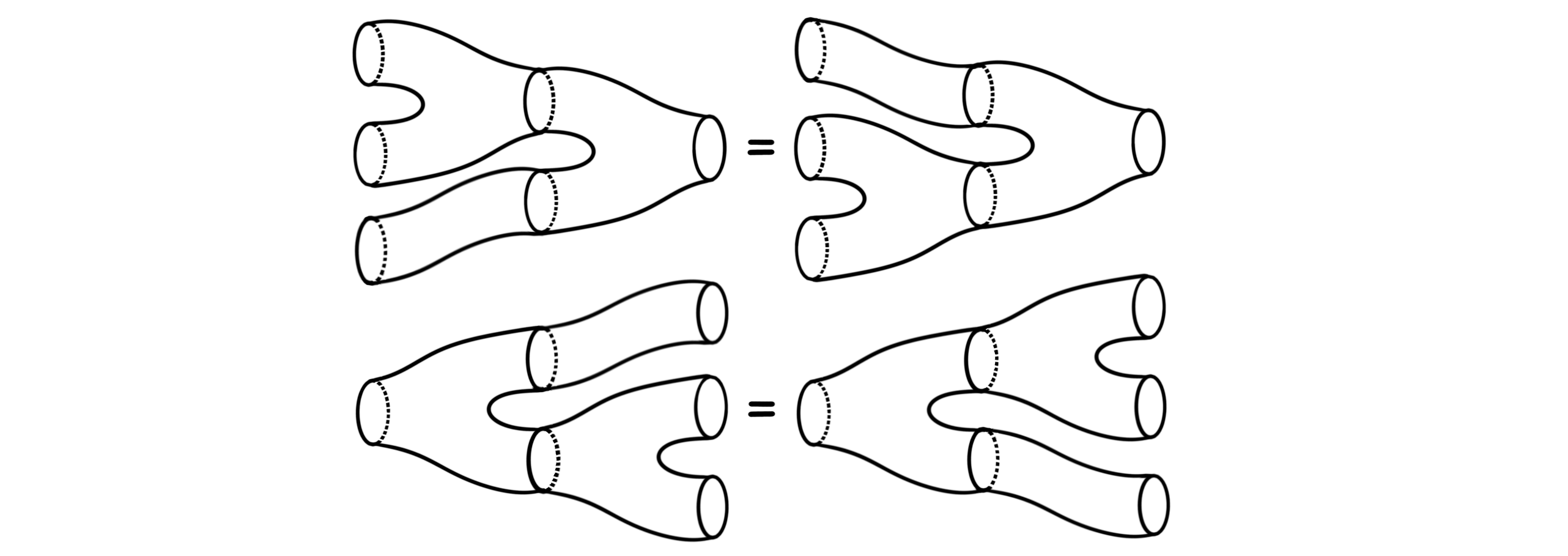
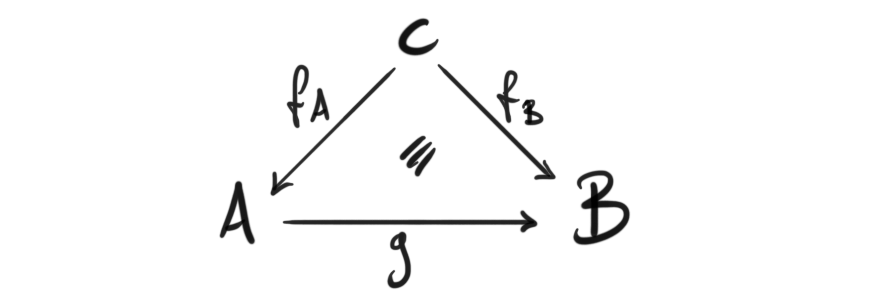
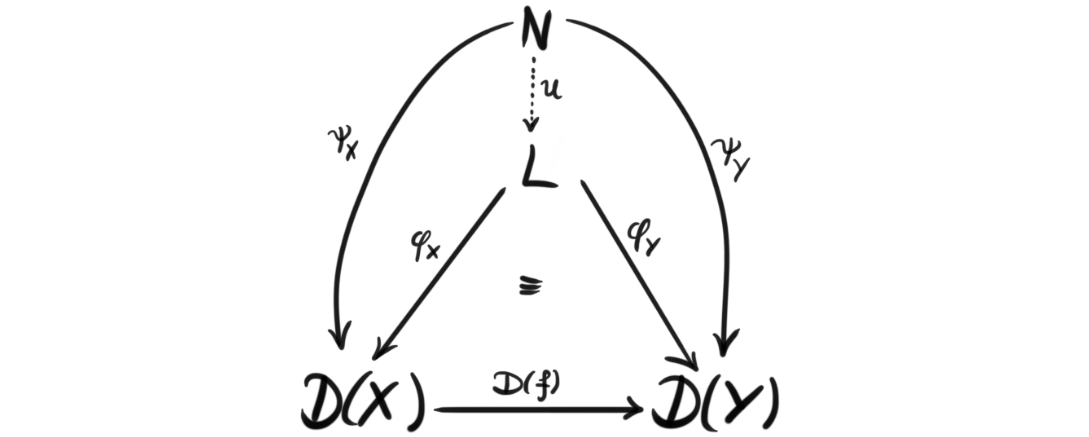
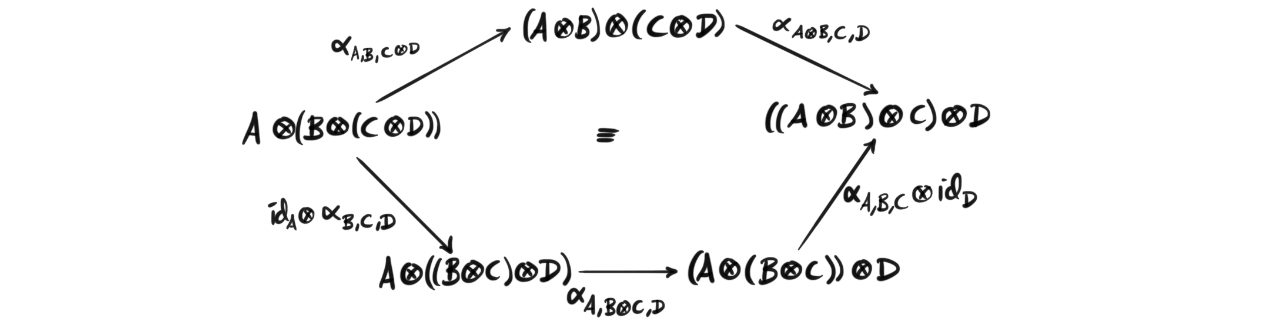
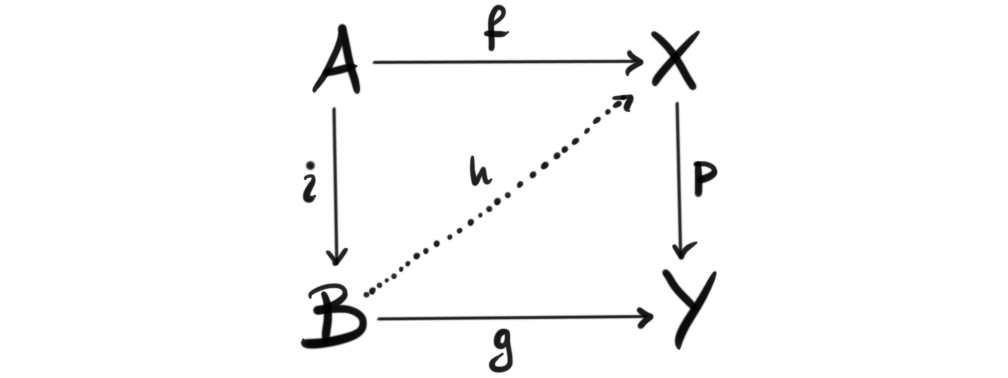
Tensor triangulated categories
For the last five years mathematics has been my passion, as well as my main focus in life. This passion for mathematics will hopefully not diminish, as I am now heading into four more years of studies and research through a PhD in mathematics at NTNU. I am joining a project, called Tensor triangulated geometry in Trondheim, so today I thought I would explore the definition of one of the main players in this theory, namely tensor triangulated categories....