This is part 7 of a series leading up to and exploring model categories. For the other parts see the series overview.
Finally we have made it to the destination we set, namely, more abstraction. This post is focused on the definition and intuition on model categories, which abstracts the objects we have been studying for some weeks, namely fibrations and cofibrations. The main definition is that of a model structure on a category, which together with a nice category will form the definition of a model category. So, why do we want this? There are more than one reason.
- Homotopy theory is not only useful for topological spaces, and can be done in other settings, for example in chain complexes. Model categories tells us when we have a category that is suitable for homotopy.
- We often talk about different homology theories or cohomology theories, but can we also have different homotopy theories?
- When working in some category, we would like to invert a nice class of morphisms, but doing so arbitrarily is not certain to give a nice result. The result will be a zig-zag of morphisms, which we in full generality have no control over. If we invert the nice morphisms in a model category however, we have nice control.
Preliminaries
As we can see, a model category is in a way a category such that its homotopy category exists and is well behaved. We will discuss this further and try to make it more precise, but before we state the definition, we need a couple preliminaries.
Definition (retraction): A map $f$ is called a retract, or a retraction of a map $g$ if there exists a diagram
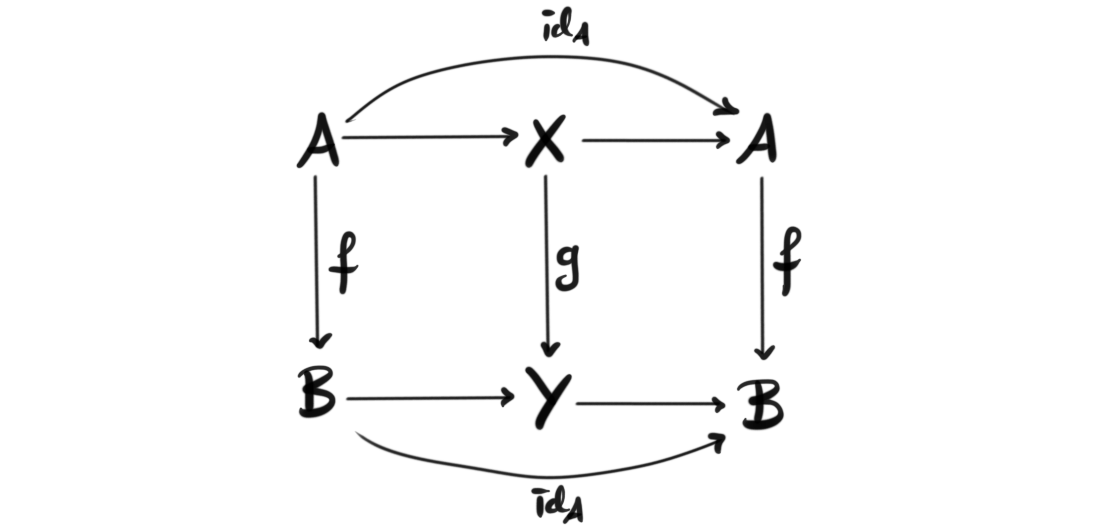
such that the horizontal maps compose to the identity map.
Definition (bicomplete category): A bicomplete category is a category where all of its small limits and small colimits exists. A small limit is a universal cone over a diagram where the index category is a set. A small colimit is similarly a universal cocone over a diagram where the index category is a set. The important feature for us will be that pullbacks and pushouts exists, and that terminal and initial objects exists. The last two will be explained better later.
Recall also that a fibration is a map that satisfies the homotopy lifting property, and that a cofibration is a map that satisfies the homotopy extension property. When we explored them earlier, it was in the setting of topological spaces, hence we could use homotopies and intervals and the like in our constructions. When we define a model category soon we can’t rely on topological spaces, since we want to obtain a general theory, not just an axiomatization of the theory of topological homotopy that we already know. But these are classes of maps that we like, and that have nice properties. Hence we want to imitate these properties in the general setting. In the formal definition, there is one more class of maps that we like, and that is called weak equivalences. We haven’t discussed these yet, but they will kind of be the isomorphisms in the homotopy theory. Think about weak homotopy equivalences, which are maps that induce isomorphisms on all homotopy groups, and quasi isomorphisms as the motivating examples.
Model categories
We now have enough backstory and preliminaries to make a precise definition of a model structure on a category. Our goal is to generalize the stage for homotopy theory, but in the definition it will not however be intrinsically clear how we are going to define homotopy, because to be general, there are no reference to a unit interval or something similar. For me it is helpful to think about the motivating example, being the category of topological spaces, when reading the definition.
Definition (model structure): A model structure on a category $\mathscr{C}$ consists of three classes of maps called fibrations, cofibrations and weak equivalences, such that the following axioms hold. To make some of the axioms easier, we call a fibration that is also a weak equivalence an acyclic fibration, and similarly we call a cofibration that is also a weak equivalence an acyclic cofibration.
MC1: Any retraction of a map in one of the three classes is again in the same class. The classes are called retraction closed.
MC2: The class of weak equivalences has the “two out of 3” property, i.e. if two out of $f, g, g\circ f$ is a weak equivalence, then the last of them is also a weak equivalence.
MC3: If we have a commutative square
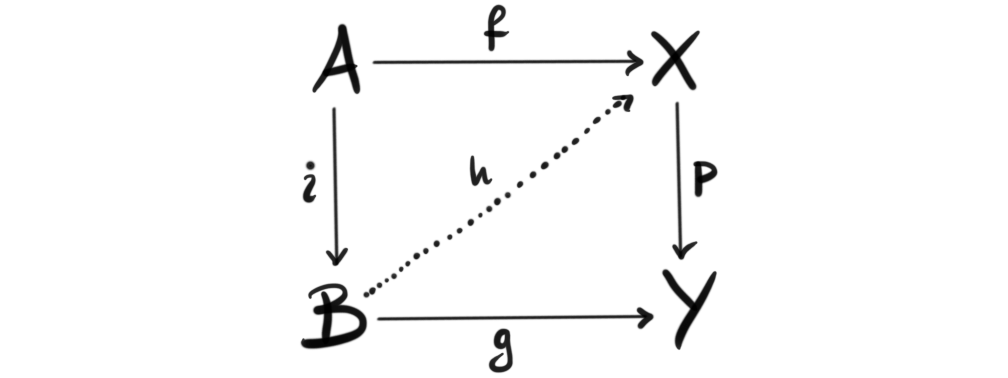
where either $i$ is a cofibration and $p$ is an acyclic fibration, or $i$ is an acyclic cofibration and $p$ a fibration, then there exists a map $h: B \rightarrow X$ making both subdiagrams commute. This is often referred to as fibrations having the right lifting property with respect to acyclic cofibrations, and cofibrations having the left lifting property with respect to acyclic fibrations.
MC4: Any map $f:X\rightarrow Y$ has two factorizations $f=p\circ i$ where $i$ is a cofibration and $p$ is an acyclic fibration, and $f=p\circ i$ where $p$ is a fibration and $i$ is an acyclic cofibration.
Definition (Model category): A model category is a bicomplete category $\mathscr{C}$ together with a model structure.
The definition seems a bit weird, and as mentioned, it has no reference to any homotopy going on, and does not give us anything extra for free. But, as time have shown since the first definition of a model category by Quillen in the 60’s, this is the correct definition. The definition we have given is a bit stricter than the original definition by Quillen, but the one presented here is equivalent to Quillens definition of a closed model category. Also, in the original formulation, the acyclic fibrations and acyclic cofibrations were called trivial fibrations and trivial cofibrations. These have been changed to avoid confusion between another term often referred to as trivial fibrations, namely fibrations where the total space is the product of the base space and the fiber. The name maybe also sound a bit weird, but it is kind of short for “the category of models”, which might make some sense. It consists of the models for where we can do homotopy, and “models” the homotopy category.
Because a model category is complete and cocomplete it has an initial object $I$ and a terminal object $T$. These are objects such that there exists an unique morphism out of, and into them respectively. If the unique morphism from an object $X\rightarrow T$ is a fibration, then $X$ is called fibrant, and if the unique morphism $T\rightarrow Y$ is a cofibration, then $Y$ is called cofibrant. We are going to define homotopy in a model category next time, but it will turn out that a proper homotopy theory will only work for a subclass of objects in the category, which are the objects that are both fibrant and cofibrant.
Examples
As I mentioned before, the important image to have in your head is the category of topological spaces, and this will also be our first example. This is complete and cocomplete, since the forgetful functor lifts both limits and colimits uniquely from the category of sets. It has more than one model structure, but the most familiar one has Serre fibrations as its fibrations and weak homotopy equivalences as its equivalences. We did not have a similar definition of cofibrations only with respect to CW complexes, so the cofibrations are not the ones we already know unfortunately. The cofibrations in this model structure is best described by being retracts of relative cell complexes, i.e. a retraction of a map $X\rightarrow Y$ where $Y$ is made from $X$ by attaching cells. Weak homotopy equivalences are the maps we mentioned earlier, that induce isomorphisms on all homotopy groups. This historically was also the motivating example.
Another model structure on the category of topological spaces comes from Hurewicz fibrations, closed Hurewicz cofibrations and regular homotopy equivalences as the weak equivalences. This was proven by Arne Strøm, and is called the Strøm model structure on topological spaces. The unique thing about this model structure, that is certainly not the usual situation, is that every object is both fibrant and cofibrant.
Another example is the category of chain complexes of modules over some ring. Here the model structure consists of quasi isomorphisms as the weak equivalences, the fibrations are degreewise projections and the cofibrations are degreewise injections with projective cokernel. The homotopy theory in this setting is the same as regular homological algebra.
Those who know homological algebra will know about projective and injective resolutions. These objects are what is called quasi isomorphic replacements, and this can also be defined in the general setting. Any morphism in the category can be factorized, so if we factorize the unique map into the terminal object $X\rightarrow T$, into a weak equivalence and a fibration. This will make a space which is weakly equivalent to $X$ and is a fibrant object. This is called a fibrant replacement of $X$. The same can be done with the unique morphism out of the initial object, which will result in a cofibrant replacement. In the example of the category of chain complexes over a ring a projective resolution is an example of a cofibrant replacement, and an injective resolution is an example of a fibrant replacement.
The notions of fibrant and cofibrant replacements will be important when we introduce homotopy in a model category and the homotopy category of a model category. There are two ways to do this, and we will explore them both. One comes from constructing homotopy classes of maps, and the other by localization at the weak equivalences. But, we will save this for next time.