This is part 2 of a series leading up to and exploring model categories. For the other parts see the series overview.

Yesterday we discussed the standard definition of a fibration by the homotopy lifting property, and today we are continuing that discussion, but in a more visual manner. This we will do by first looking at fiber bundles, and then generalizing them. Since fibrations are generalized fiber bundles, every fiber bundle is an example of a fibration, and they have been the most important examples for me, as they help me visualize and get intuition into the fibrations without having to really use the full generality of the definition. The main idea of a fiber bundle is that of a family of topological spaces parameterized by another topological space. This family will again form a topological space usually called the total space of the fiber bundle, while the space that parameterizes it is called the base space. Before we get rigorous and technical with definitions, we explore an example.

Examples and intuition

The best two “starter examples” for me at least is the cylinder, and the Möbius band. How are these a family of topological spaces parameterized by another space you ask? They can both can be thought of as a collection of intervals parameterized by a circle. The following picture of the cylinder might make it more clear.

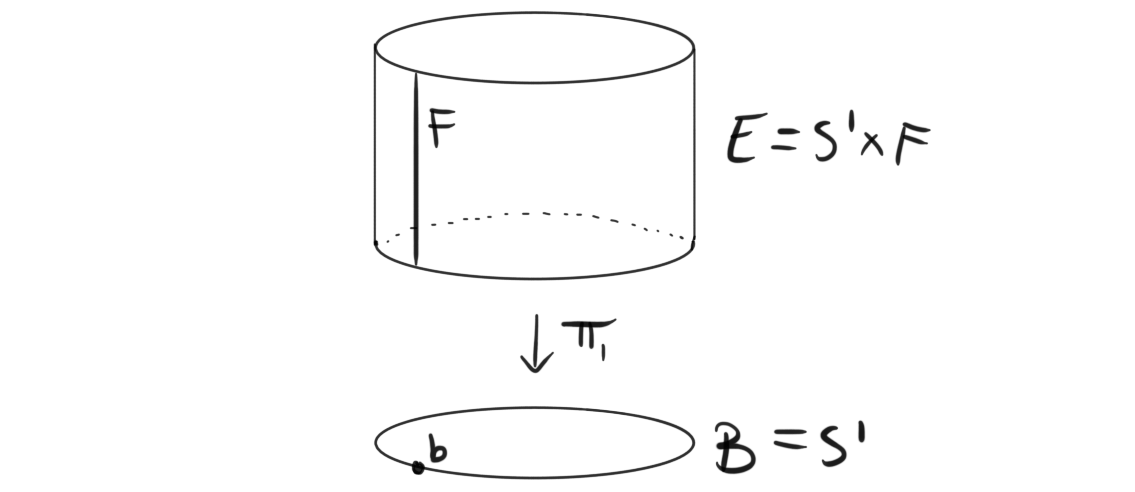
For every point on the circle $S^1$ we have an interval $F$ “above” that point. The map $\pi_1$ from the cylinder to the circle is just the projection map $\pi_1:S^1\times I \rightarrow S^1$, which then gives us our first example of a fibration, namely projections. We call the cylinder a fiber bundle over $S^1$ with typical fiber $F$ , or sometime an $F$ -bundle over $S^1$ . If we instead look at the Möbius band it is a bit more complicated, but not much. We again give a picture.

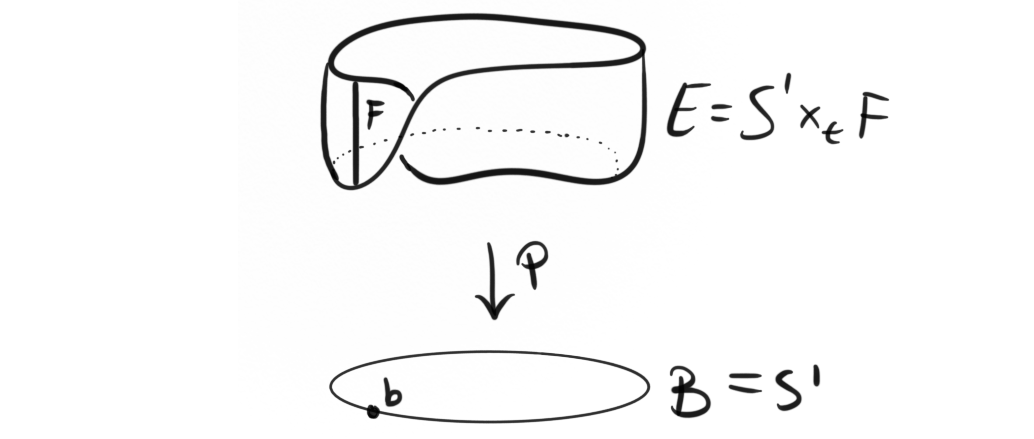
We see the same phenomenon as with the cylinder. Above every point on the circle we have a copy of the interval $F$ , but the difference is that this is no longer just the usual projection. We have a twist, which makes it a bit weirder, hence the Möbius band is equal to the twisted product $M= S^1\times_t F$ . But, we see that can make it into the projection locally, and this is the key to understand fiber bundles. Now, what does it mean that a map is a projection locally? It means that on the inverse image of open sets in $B$, the map $p$ restricted to that inverse image is just the projection.

Definition and relation to fibrations

In fact, in a fiber bundle we allow slightly more, we allow that it is locally a projection up to a homeomorphism. This is just saying that we allow some topological variation of the fibers, and that a fiber bundle is a topological object and not totally rigid because we allow deformations and continuous “disturbances” in $E$ . This is also reflected in the proper definition.

Definition (fiber bundle): A map $p:E\rightarrow B$ is called a fiber bundle with typical fiber $F$ if for every point $b\in B$ , there exists an open set $U$ around $b$ and a homeomorphism $h:p^{-1}(U)\rightarrow U\times F$ such that $p_{|p^{-1}(U)}= \pi_1 \circ h$ , where $\pi_1$ is the projection onto the first component.

Now that we have an ok understanding of fiber bundles we can ask how they relate to fibrations. I said last time that in a fibration, every fiber is homotopy equivalent, and this is the generalization. In a fiber bundle, all fibers are homeomorphic. We can see this because $\pi_1^{-1}({b}) \simeq F$ , and hence $p^{-1}({b}) \simeq F$. If we instead require this to be a homotopy equivalence we get a fibration. Since all homeomorphisms are homotopy equivalences, all fiber bundles are fibrations.

Now we know both the standard technical definition of a fibration, and we know how to visualize them and think about them. What remains is to learn how to use them, and this we will do in the upcoming posts. I will have one post for the long exact sequence of homotopy groups, and one for the spectral sequence associated to a fibration.