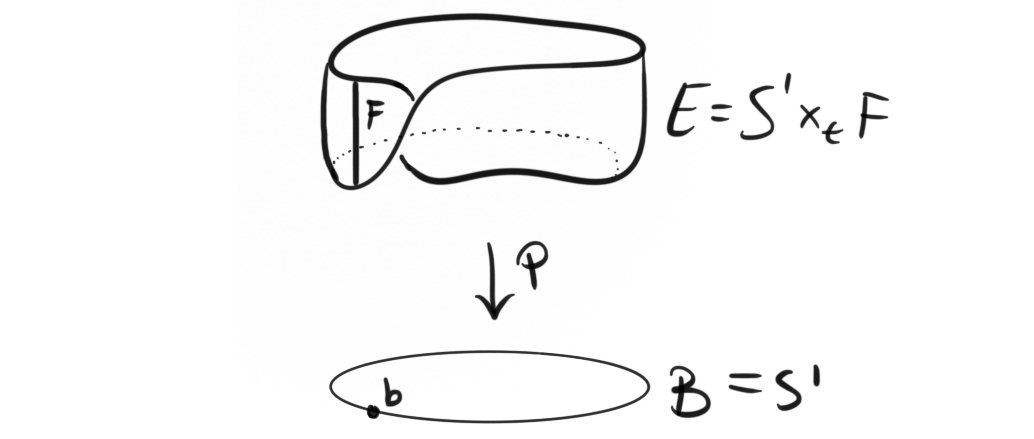
Swan's theorem
A part of mathematics I really an starting to enjoy more is mathematics that explain or develop connections between geometry or topology, and algebra. The first two posts on this blog was focused on developing some geometrical insight to two lemmas from commutative algebra, namely Noether’s normalization lemma and Zariski’s lemma. There are many more such connections worth discussing and exploring, and today I want to focus on one of these “bridges” between geometry and algebra, namely Swan’s theorem....