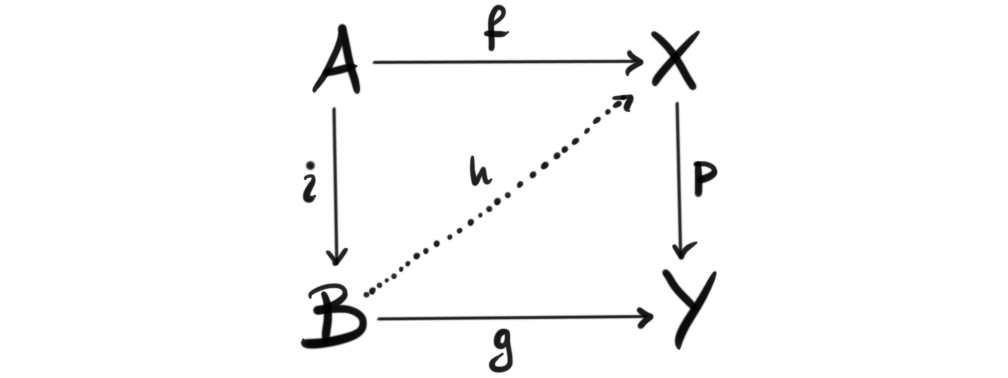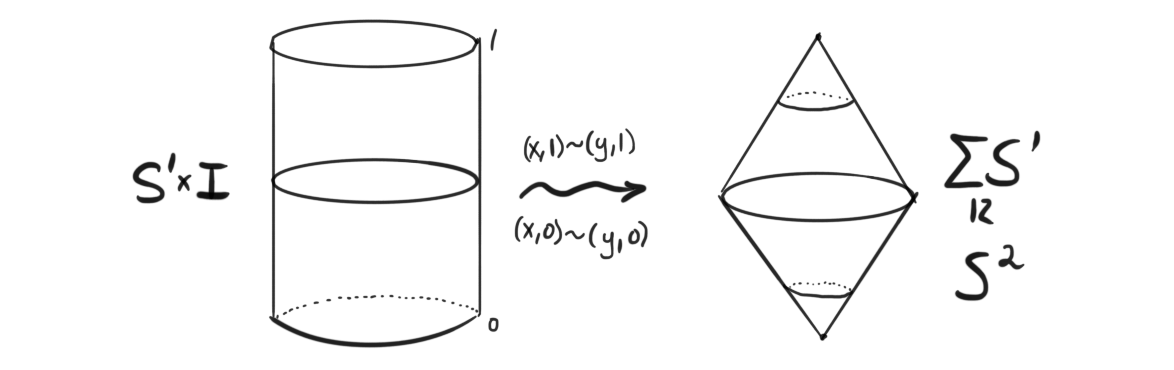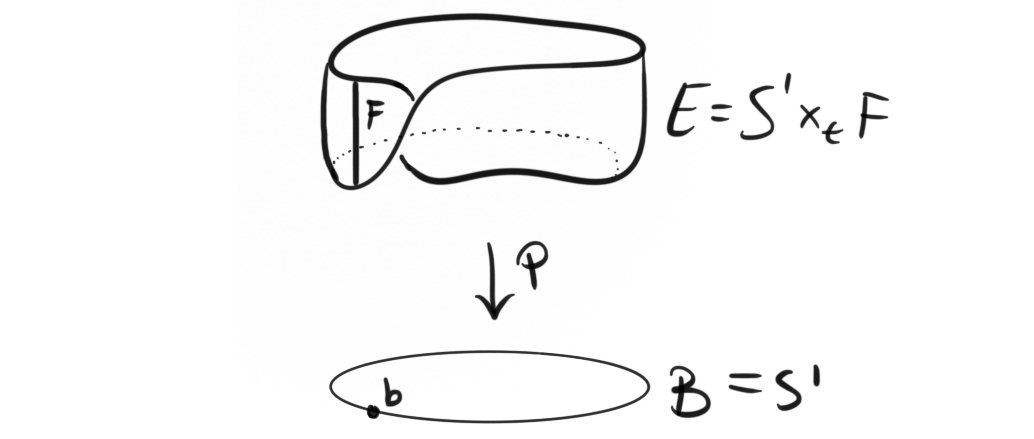
Homotopy in model categories
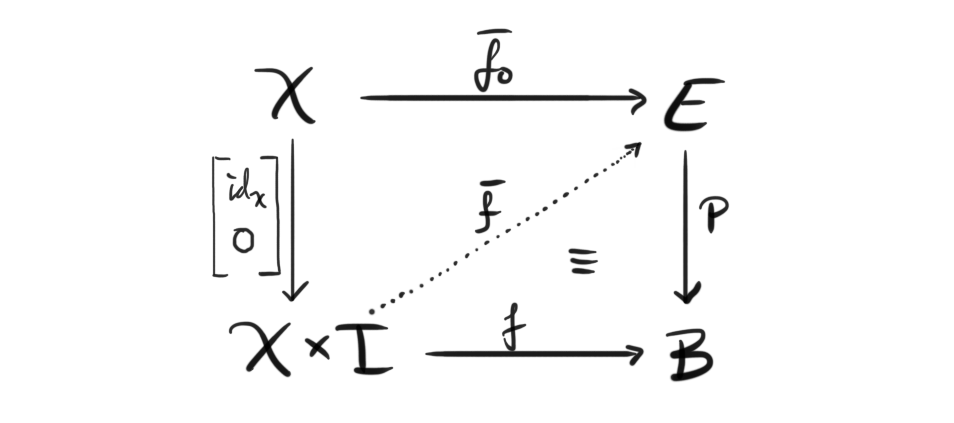
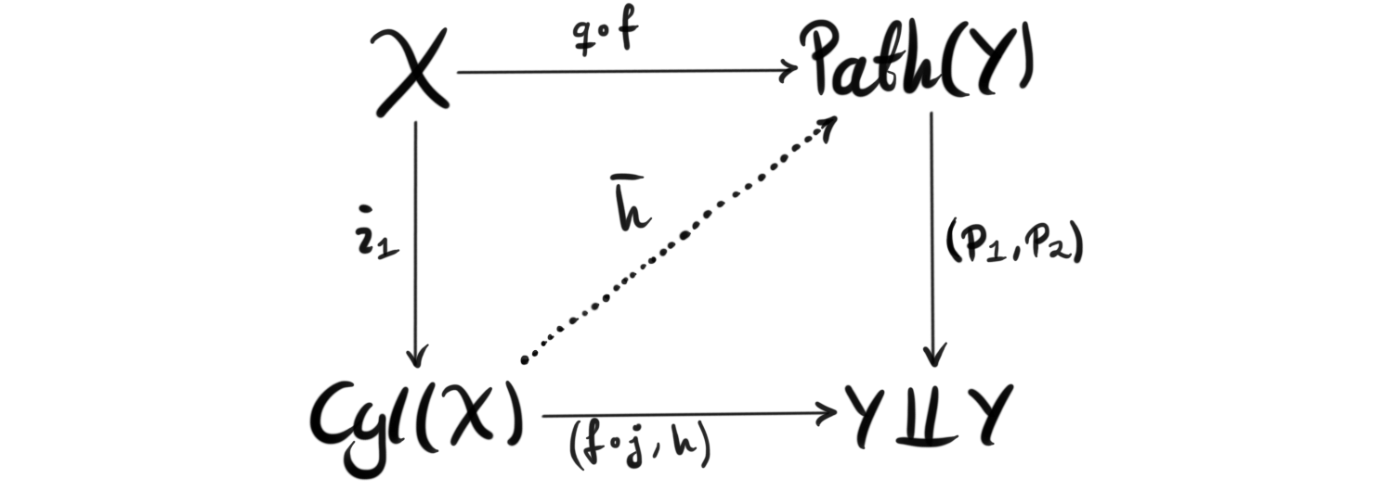
This is part 8 of a series leading up to and exploring model categories. For the other parts see the series overview. Last time we finally defined the model category, gave some examples and tried (kind of) to give a motivation to why they are interesting and how they set the stage for homotopy theory. The first time I read the definition I was a bit confused about the lack of mention of homotopy, or at least some prototype of it that I could connect with....