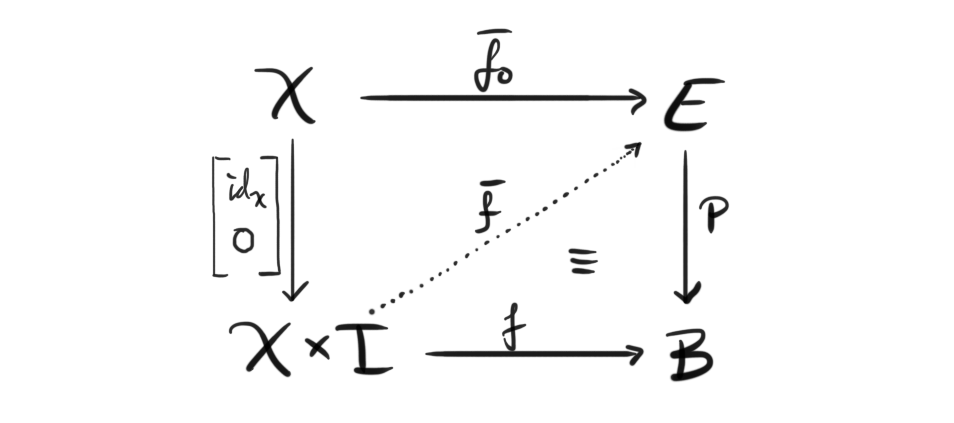
Fibrations
This is part 1 of a series leading up to and exploring model categories. For the other parts see the series overview. My main mathematical interest for the last couple years has been algebraic topology. I feel it suits my needs for intuition, and graphical picturing of what happens. A concept I have been learning more rigorously recently is fibrations, and how to use them in computing homotopy groups and homology groups of different spaces....