Introduction
This spring I have been taking a graduate class in commutative algebra, and I have yet to do algebraic geometry in a proper way, and have only gotten a small taste while writing my bachelor thesis. So this entire semester, I have felt this hinting at a geometric picture from the algebra itself, but i didn’t have the insight to figure it out. That said, I now think I have the geometric picture for Noether normalization, which in term implies a geometric picture of Hilbert nullstellensatz and some other results. It took a long time to convert the algebra into geometry for me, and i still have much to learn regarding this. What i have started to figure out is the close relationship between ideals and varieties. I have for a while known that this is one of the main reasons to introduce commutative algebra into algebraic geometry, but i couldn’t see the picture myself. Anyway, lets start with some introductory stuff.
An affine algebraic variety $X$ in $k^n$ is a subset of $k^n$ cut out by a collection of polynomials $F=\{ f_i\}_ {i\in I}$, i.e. $X = \{ x\in k^n \vert f_i(x)=0, \forall f_i \in F\}$. The set $F$ of polynomials generate a prime ideal of $k[x_1, \cdots, x_n]$, which we denote by $I(X)$. We can also start by taking a prime ideal $\mathfrak{p}$ in $k[x_1, \cdots, x_n]$ and generate its vanishing set $V(\mathfrak{p})$, which will be it’s corresponding affine algebraic variety. More explicitly $V(\mathfrak{p})= \{ x\in k^n \vert f(x)=0, \forall f\in \mathfrak{p}\}$. The ring $P(X)=k[x_1, \cdots, x_n]/I(X)$ is called the coordinate ring of the variety. This correspondence is the key bridge between the geometric picture and the algebra, and the full relation is described by Hilbert’s nullstellensatz.
Geometry of normalization
Before I explain the geometric meaning i have learned, I want to formulate the lemma in the regular algebraic way it is usually presented.
Lemma (Noether): Let $k$ be an algebraically closed infinite field and $A$ a finitely generated $k$-algebra. Then there exists an integer $d $ and algebraically independent generators $y_1, \cdots ,y_d $ such that $A $ is a finitely generated module over $k[y_1, \cdots, y_d] $.
It is often useful to know weather an affine algebraic variety $X$ projects onto a linear subspace of $k^n$. This can for example tell us information on the dimension of the variety, which again tells us other useful stuff. I have not yet explored dimension theory, hence the motivation behind this is maybe still a bit vague to me. This projection induces an injection on the cordinate rings. Let $A$ be the coordinate ring of an affine algebraic variety $X$ and $B$ the coordinate ring of a linear subspace $L$ of $k^n.$ By a coordinate change, $L \cong k^d$, hence $I(L)$ is the zero ideal, because it consists of all polynomials in $d$ variables who vanish on every point in $k^d$, which is only the zero polynomial. Hence the coordinate ring $B$ is isomorphic to $k[x_1, \cdots x_d] $.
A given projection $X \longrightarrow L$ then induces an injection $k[x_1, \cdots, x_d]\longrightarrow P(X) $, and a natural question that arises (somehow) is when is this injection a finite morphism. By definition this is the same as asking when $P(X) $ is a finitely generated module over $k[x_1, \cdots, x_d] $ or when $P(X) $ is an integral extension of $k[x_1, \cdots, x_d] $. Noether’s normalization lemma tells us that this is the case when the projection $X \longrightarrow L $ is surjective.
I’m not going to prove the lemma, but i will instead present an explicit example. Let $k=\mathbb{R} $ and let $X $ be the variety defined by $x\cdot y = 1$ in $\mathbb{R}^2 $. This is a hyperbola with asymptotes along the $x$ and $y $ lines. If we take $L$ to be the linear subspace generated by $x$, i.e. the $x$-axis, then the canonical “straight down” and “straight up” projection hits the whole line except the origin.
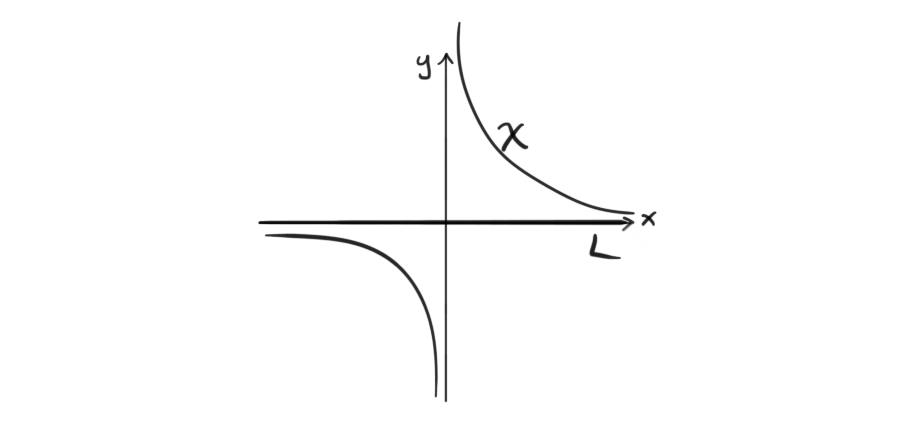
Now, what does this mean for our induced injection? The coordinate ring of $L$ is just $\mathbb{R}[x]$ while the coordinate ring of $X$ is $P(X) = \mathbb{R}[x, y]/(xy-1)$, hence we have the injection $\mathbb{R}[x] \longrightarrow \mathbb{R}[x, y]/(xy-1) $. If this was an integral extension, then every prime ideal of $\mathbb{R}[x] $ would have a prime ideal of $\mathbb{R}[x, y]/(xy-1)$ laying over it, but there is no prime ideal in $\mathbb{R}[x, y]/(xy-1)$ over the ideal generated by $x$, since all ideals in $\mathbb{R}[x, y]/(xy-1)$ that contain $x $ must be the whole ring. Hence it can’t be an integral extension.
But, notice here that we in fact can do a linear coordinate change by rotating our axis $45^\circ $, i.e. $x' = x+y $ and $y' = x-y $. Now the same projection is a surjection which in theory should make the injection an integral extension.
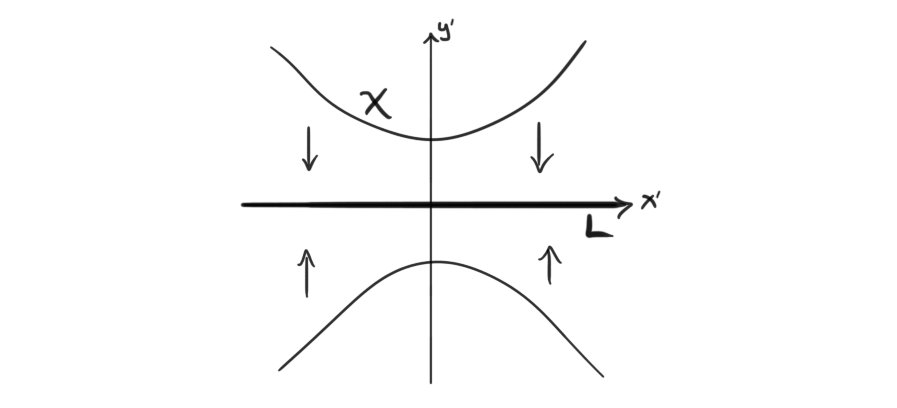
The coordinate change gives us $x = \frac{x'+y'}{2} $ and $y = \frac{x'-y'}{2} $, thus we get $0 = xy-1 = \frac{(x'-y')(x'+y')}{4} -1 = x'^2 - y'^2 - 4 $. Hence our coordinate ring in the new generators is $\mathbb{R}[x', y']/(x'^2 - y'^2 - 4) $. Now we see that this ring is integral over $\mathbb{R}[x'] $ since we have a monic polynomial $f(t) = t^2 - (\overline{x'}^2+4) $ which is zero at $y'$. Here $\overline{x'} $ is the image of $x' $ in the ring $\mathbb{R}[x', y']/(x'^2 - y'^2 - 4) $. Hence we have confirmed the lemma by an example. We made the integralness of $P(X) $ over $P(L) $ dependent of the projection, which is what we wanted.