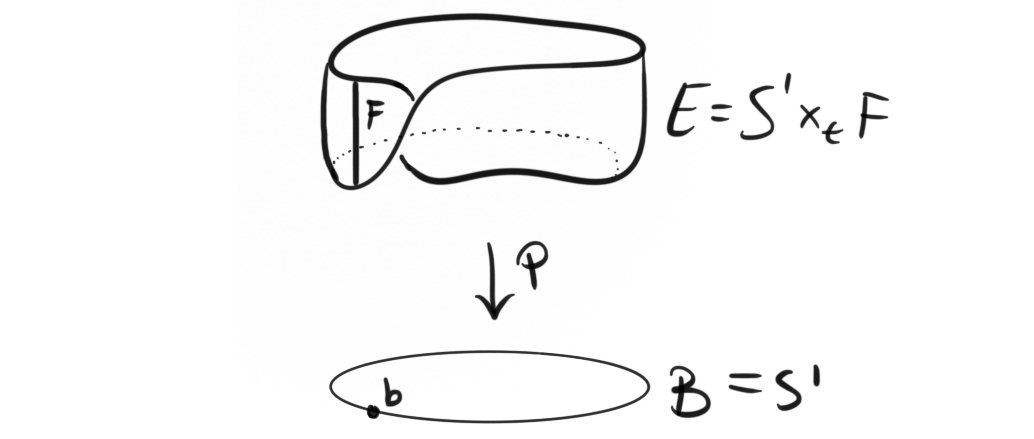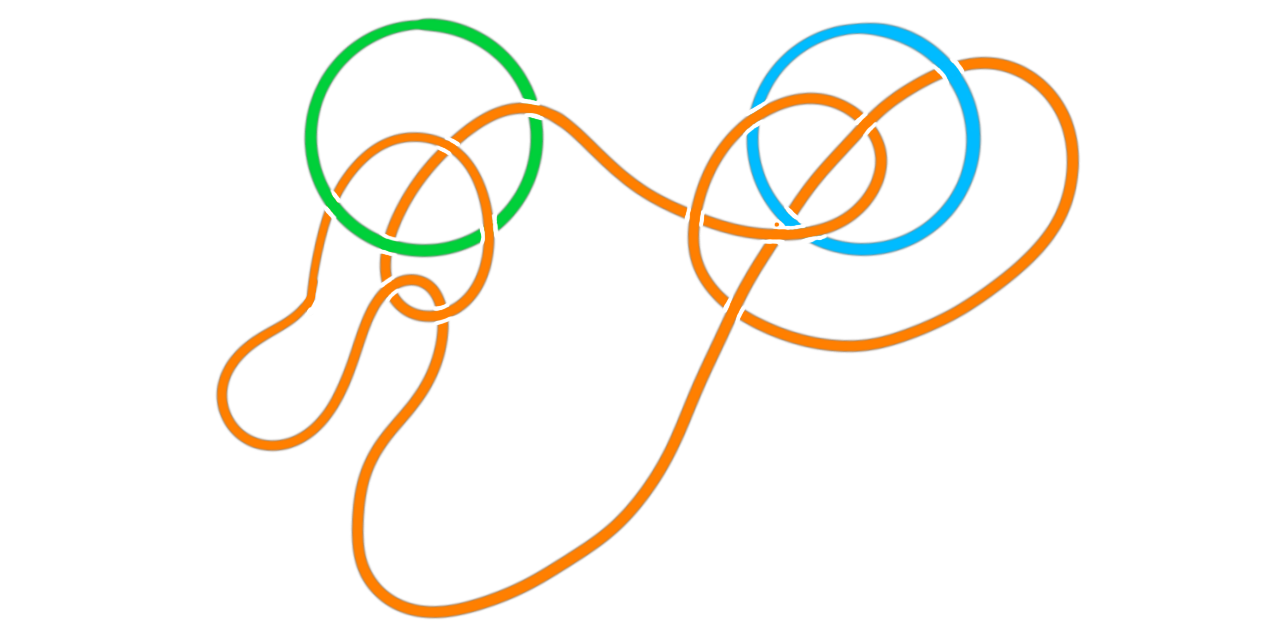
Hanging pictures with knots
Last year I posted a blog post where we looked at a way to use elementary homotopy theory to hang a picture on the wall in a stupid way. The task was to hang a picture on two nails in such a way that if we pull one of the nails out, the picture falls down. “That is stupid” I hear you say, but premise is as premise does, or something similar quoted from Forrest Gump....