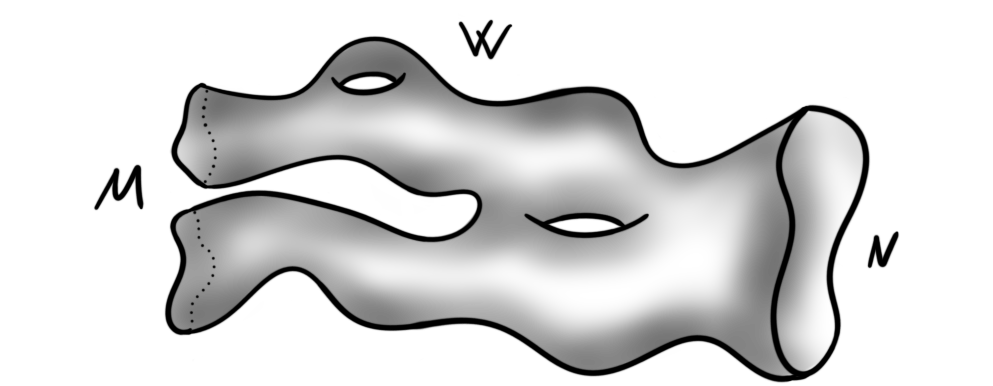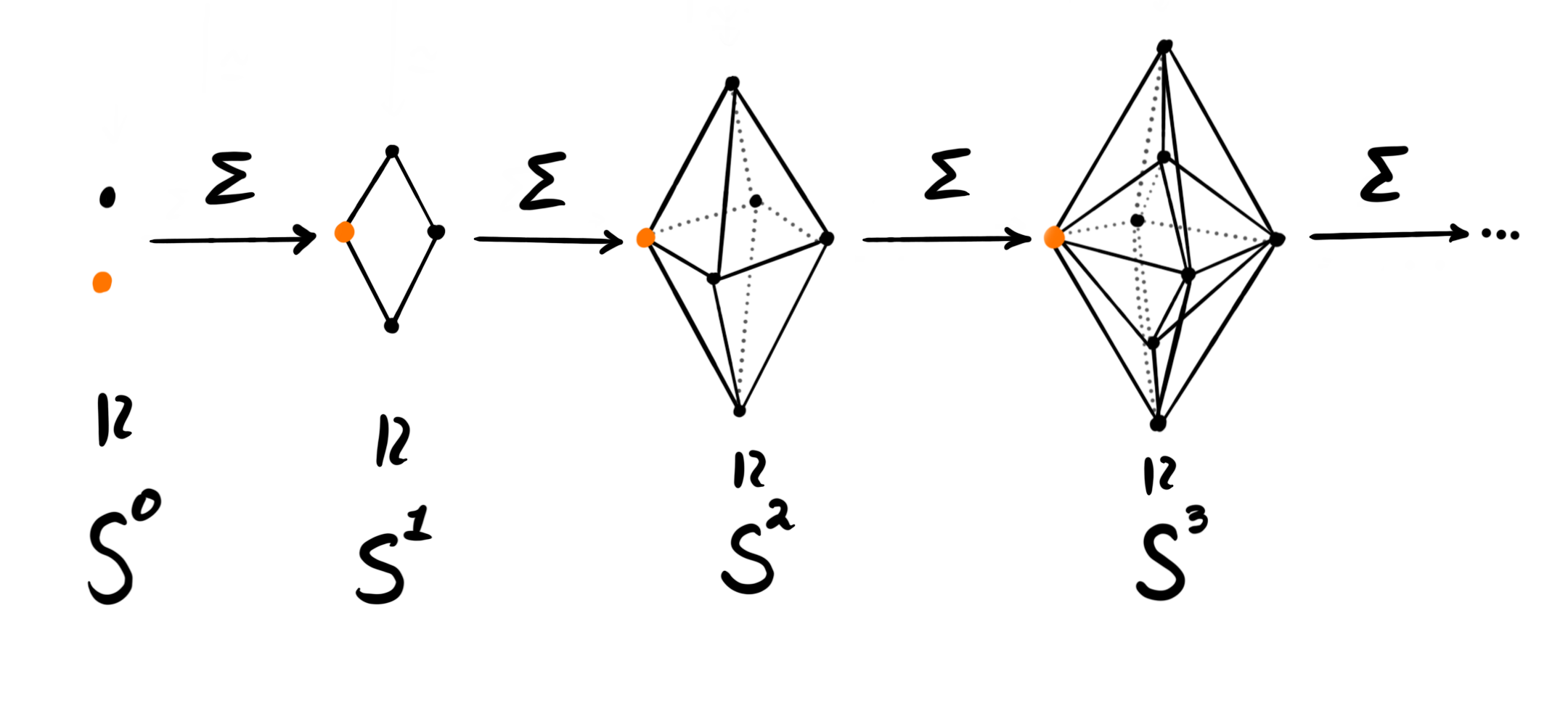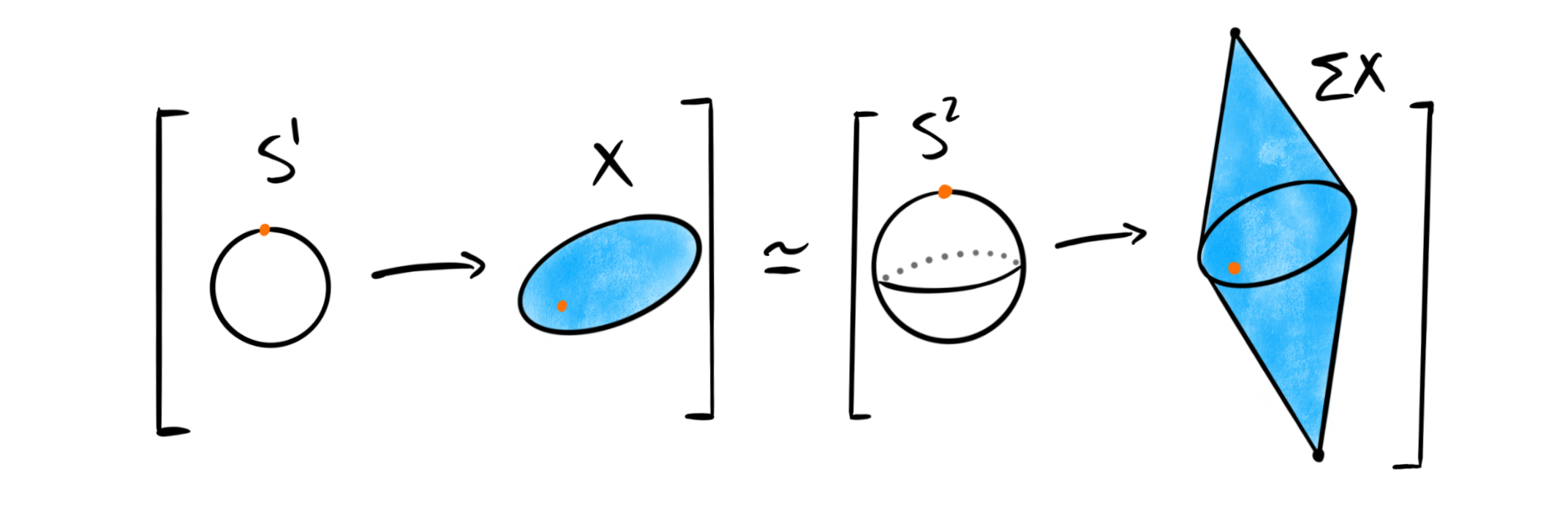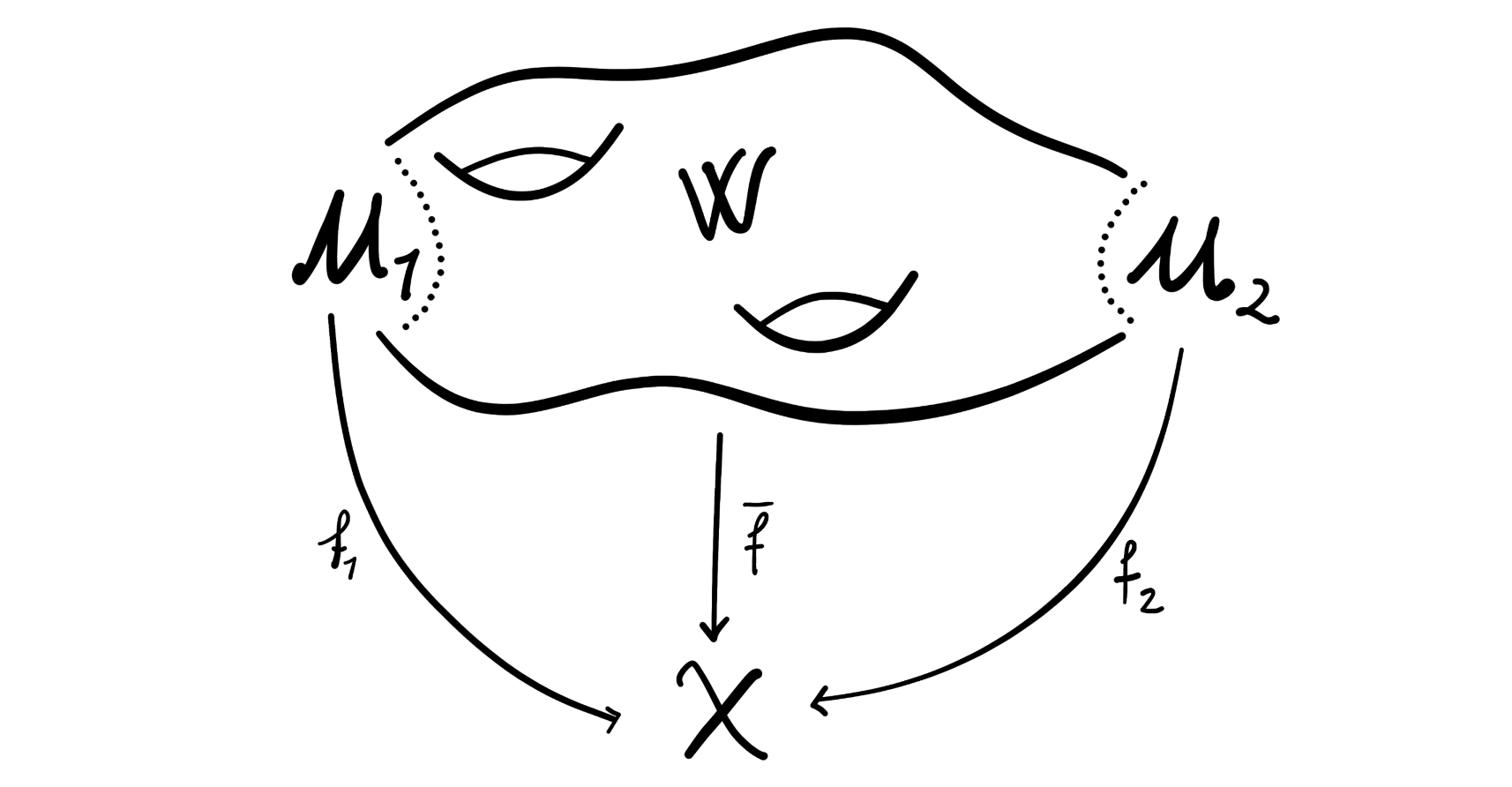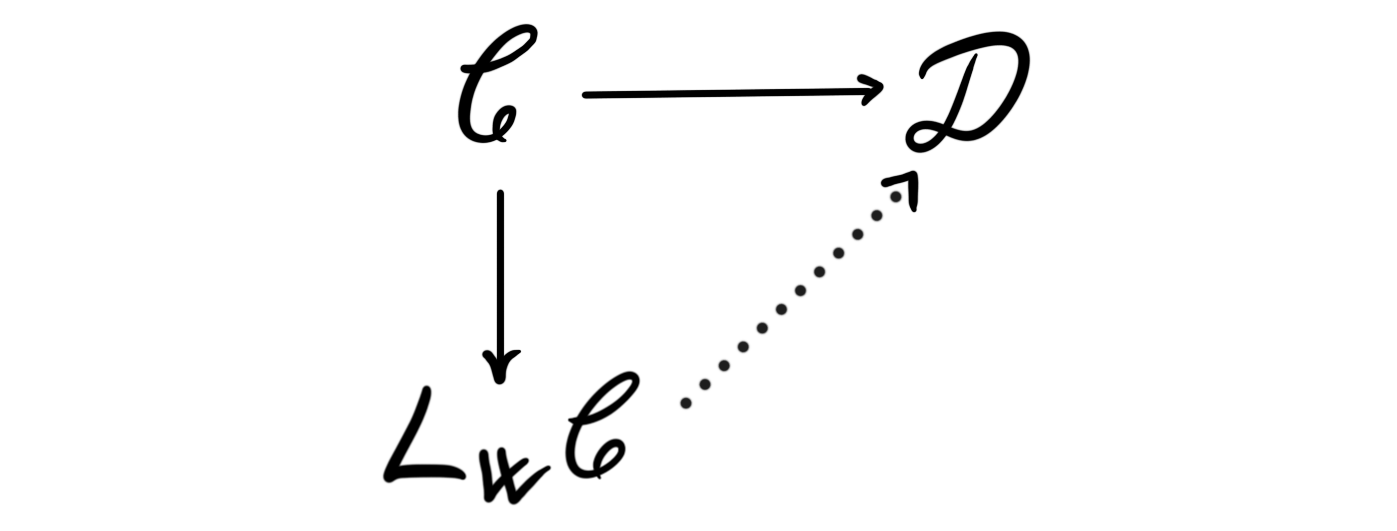
Bousfield localization
Topology, particularly homotopy theory, is hard. The scenes where these kind of mathematics happen are immensely complicated; the category of topological spaces; the category of spectra. The problem is that there is simply too much information to try to capture by using simple tools that we can actually understand properly. Trying to classify topological spaces or spectra is a feat that many deem impossible, it is simply too difficult. So, how can we try to fix this?...