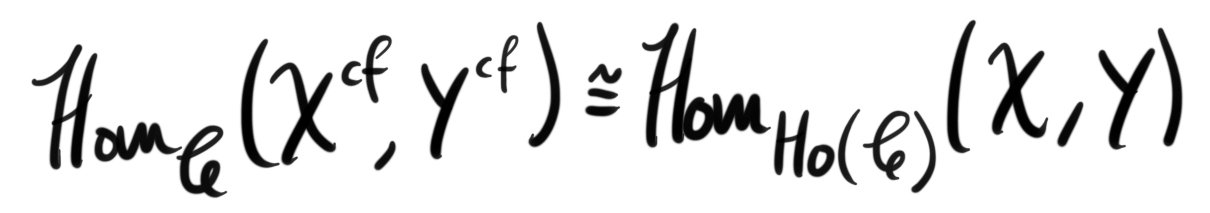How can we use travel-journaling to study some highly abstract and highly complicated mathematical machinery? Can we get anything out of such an analogy? In this post we do just that, study the homotopy hypothesis and infinity groupoids through the lens of a travel ledger.
I have recently handed in and defended my master thesis in mathematics, so I though I would go through its abstract and try to explain what it’s all about. We look at formality of DG-algebras, Massey products, A_infinity-algebras and how we can use these to some interesting results.
This is part four in a sort of connected story about operations in mathematics that are associative up to homotopy. It will probably be beneficial to read part 1, part 2 and part 3 in advance of this, but it is not required in theory. These previous posts do however build up some intuition and motivation for the object we are looking at today. To quickly recap what we already seen in these previous posts we recall that we started out by looking at how to transfer a group structure on a topological space through an isomorphism....
In the two last posts we have been discussing operations that are associative up to homotopy, and where such operations might arise naturally in topology. One claim I made, which I later realized was maybe a bit unmotivated and in need of some clarification was how some higher arity maps actually defined (or were defined by) homotopies between combinations of the lower arity maps. We also purely looked at this in a topological setting, but in algebraic topology we often translate to algebraic structures, so I also wanted to see clearly that the same constructions hold in that setting....
Imagine we have a system of two topological spaces $f:T\longrightarrow G$. We are often interested in knowing if a certain property on the space $G$ can be transferred through f such that we have the same property on $T$. If f is a nice enough morphism an example could be a topological invariant of $G$, for example its Euler characteristic. In this post we are more interested in transferring other things than invariants, more specifically structures....
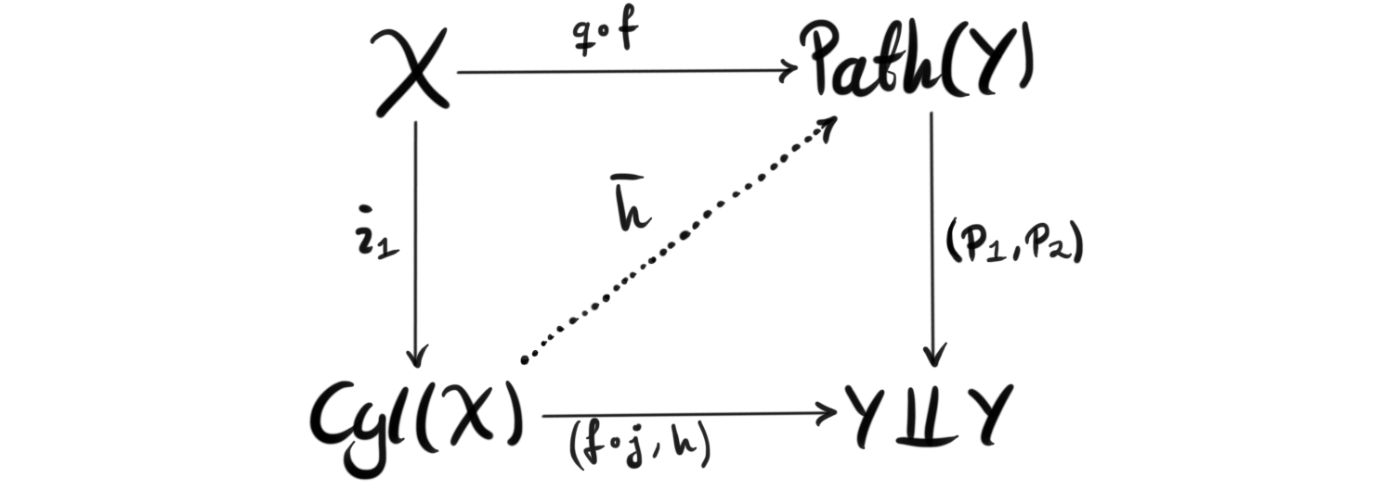
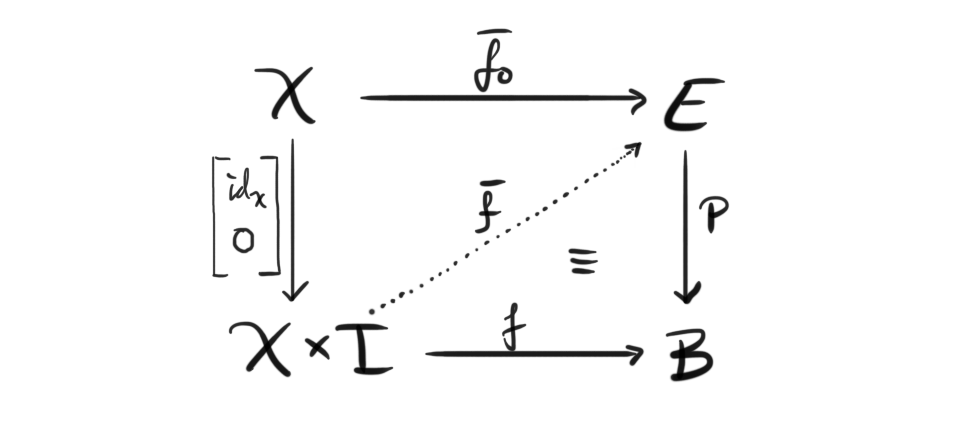
The last few posts have all been of relatively long length and have all taken some time to construct and write. I initially also wanted to produce shorter posts just discussing an example or a calculation etc, and today I tried to do just that, but failed. The post became somewhat longer than intended, but it is really informal and intuitive, so its fine in my opinion. In a previous post we discussed both weak homotopy equivalences and regular homotopy equivalences, and we have also encountered the Whitehead theorem, which says that any weak homotopy equivalence between CW-complexes is in fact a regular homotopy equivalence....
This is part 9 of a series leading up to and exploring model categories. For the other parts see the series overview. Last time we ended by giving a definition of a homotopy between maps on the collection of bifibrant objects in a model category. Today we are going to expand further upon this idea, and try to build the theory we are familiar with for topological spaces but in the general setting....
This is part 8 of a series leading up to and exploring model categories. For the other parts see the series overview. Last time we finally defined the model category, gave some examples and tried (kind of) to give a motivation to why they are interesting and how they set the stage for homotopy theory. The first time I read the definition I was a bit confused about the lack of mention of homotopy, or at least some prototype of it that I could connect with....
Some time ago I saw this problem of hanging a picture on the wall using a string and two nails in such a way that if you remove one of the nails from the wall, the picture falls down. This is a bad way to hang pictures you immediately say, and I would agree. I saw some solution to the problem, and didn’t think about it for many years, until this week when I figured out that we need homotopy, in particular the fundamental group, to do it!...
This is part 1 of a series leading up to and exploring model categories. For the other parts see the series overview. My main mathematical interest for the last couple years has been algebraic topology. I feel it suits my needs for intuition, and graphical picturing of what happens. A concept I have been learning more rigorously recently is fibrations, and how to use them in computing homotopy groups and homology groups of different spaces....