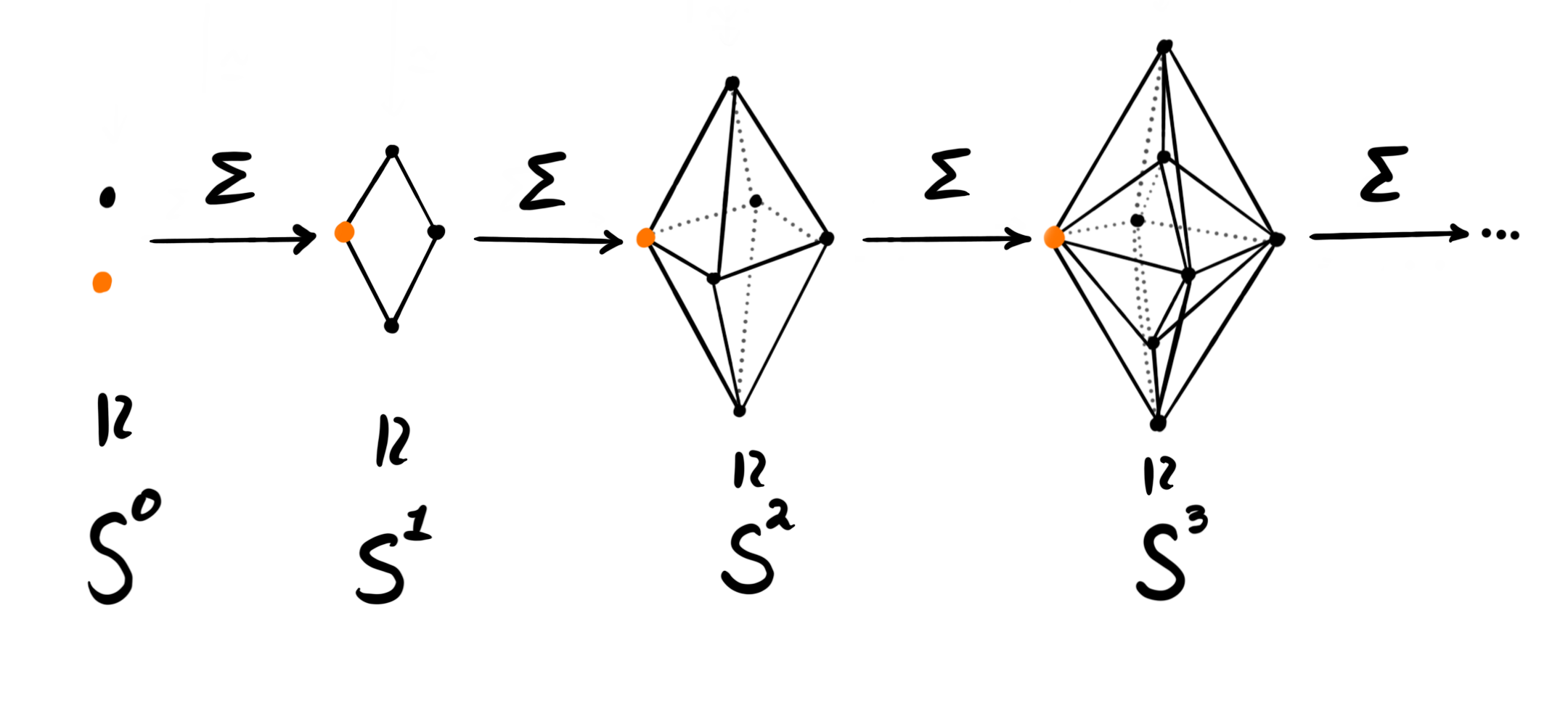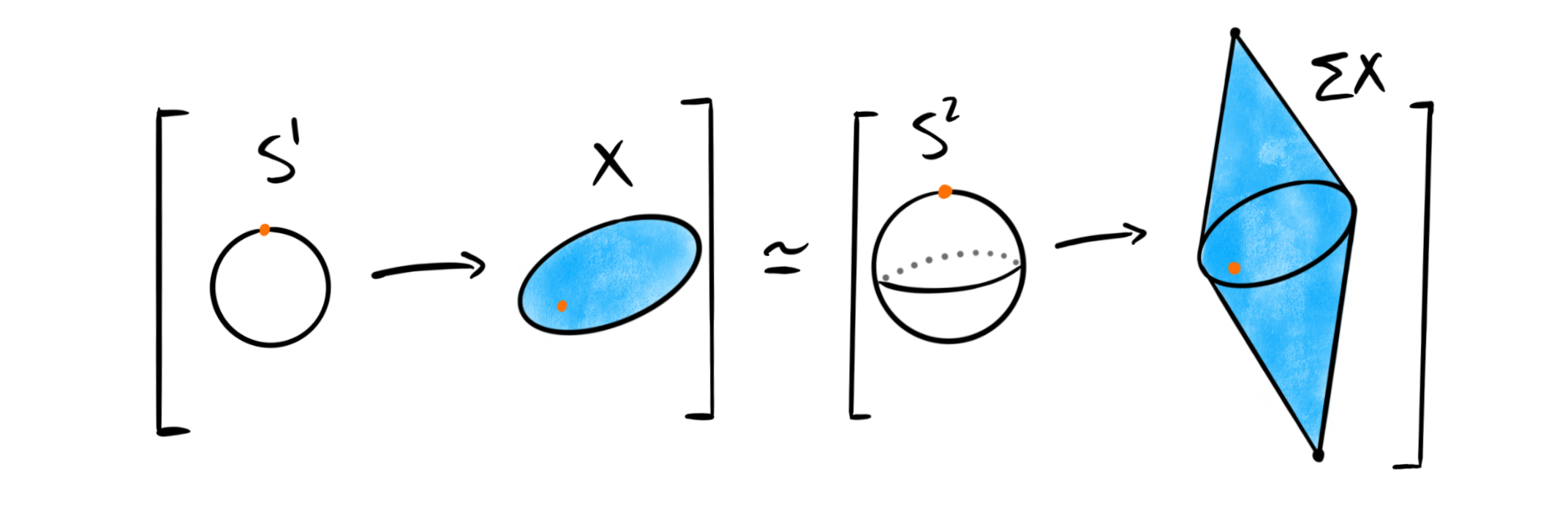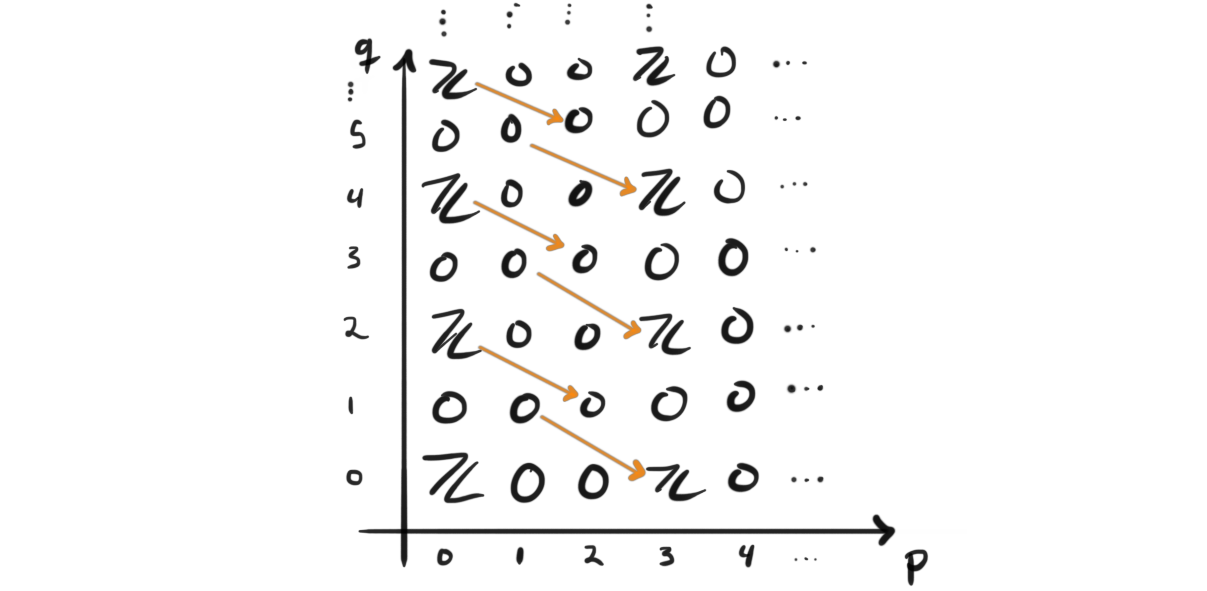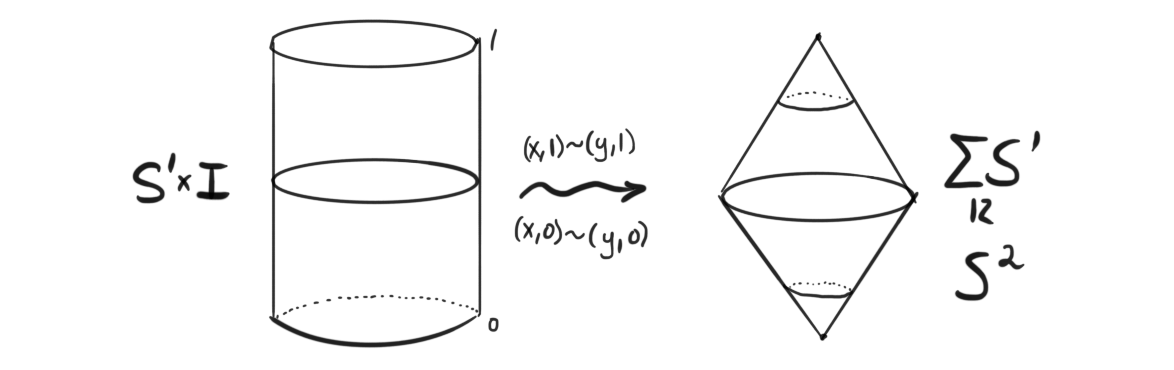
The Adams spectral sequence
Recently my friend Elias started his own math blog adventure, and his first post gave a nice introduction to spectral sequences. Reading it I remembered that I should really understand some of the parts better myself, because a lot of the arguments one makes in chromatic homotopy theory are based on spectral sequences. There is a framework for constructing spectral sequences that are not covered in my old post on them, as well as Elias’ post, and that is creating spectral sequences from exact couples....