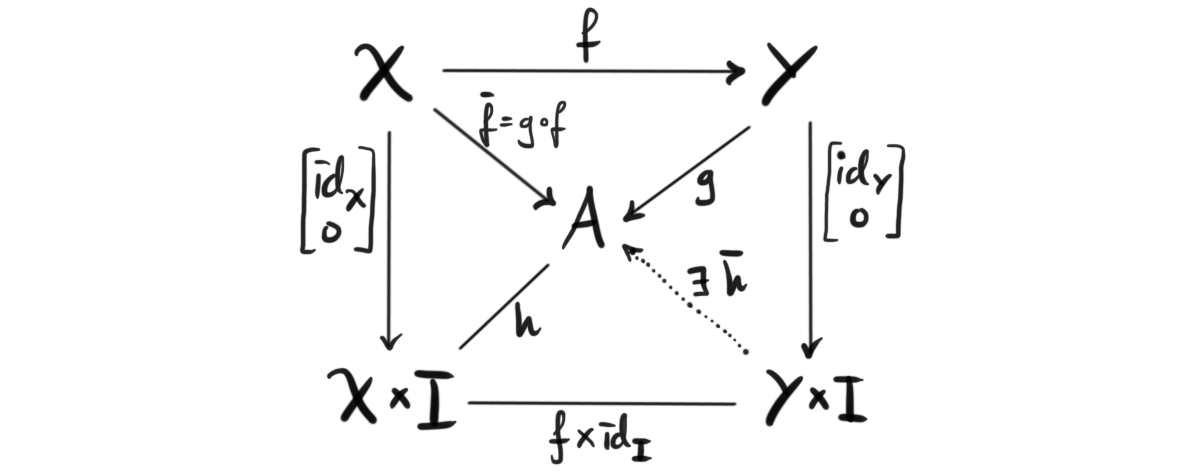
Cofibrations
This is part 6 of a series leading up to and exploring model categories. For the other parts see the series overview. Through the series so far we have covered the basic uses of fibrations and related things, like the long exact sequence of homotopy groups, the Serre spectral sequence, fiber bundles and homotopy groups of spheres. But, we have not mentioned that fibrations has a dual construct, namely cofibrations. The road we are heading with this series, as mentioned before, is to define Model categories, and discover how to use them....