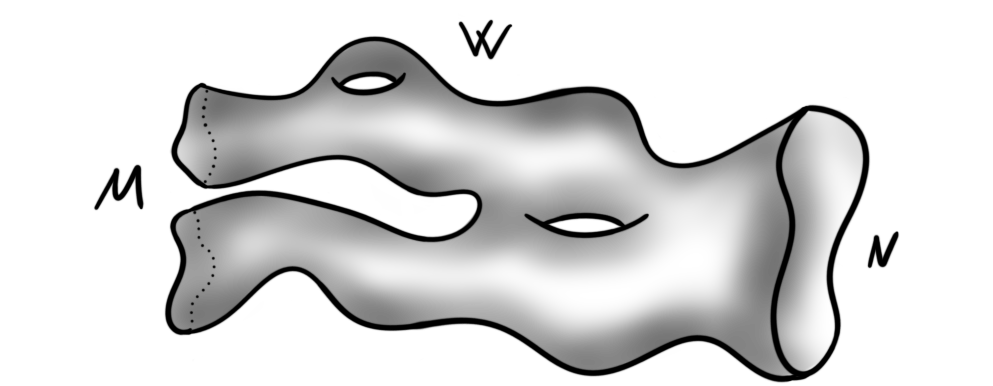
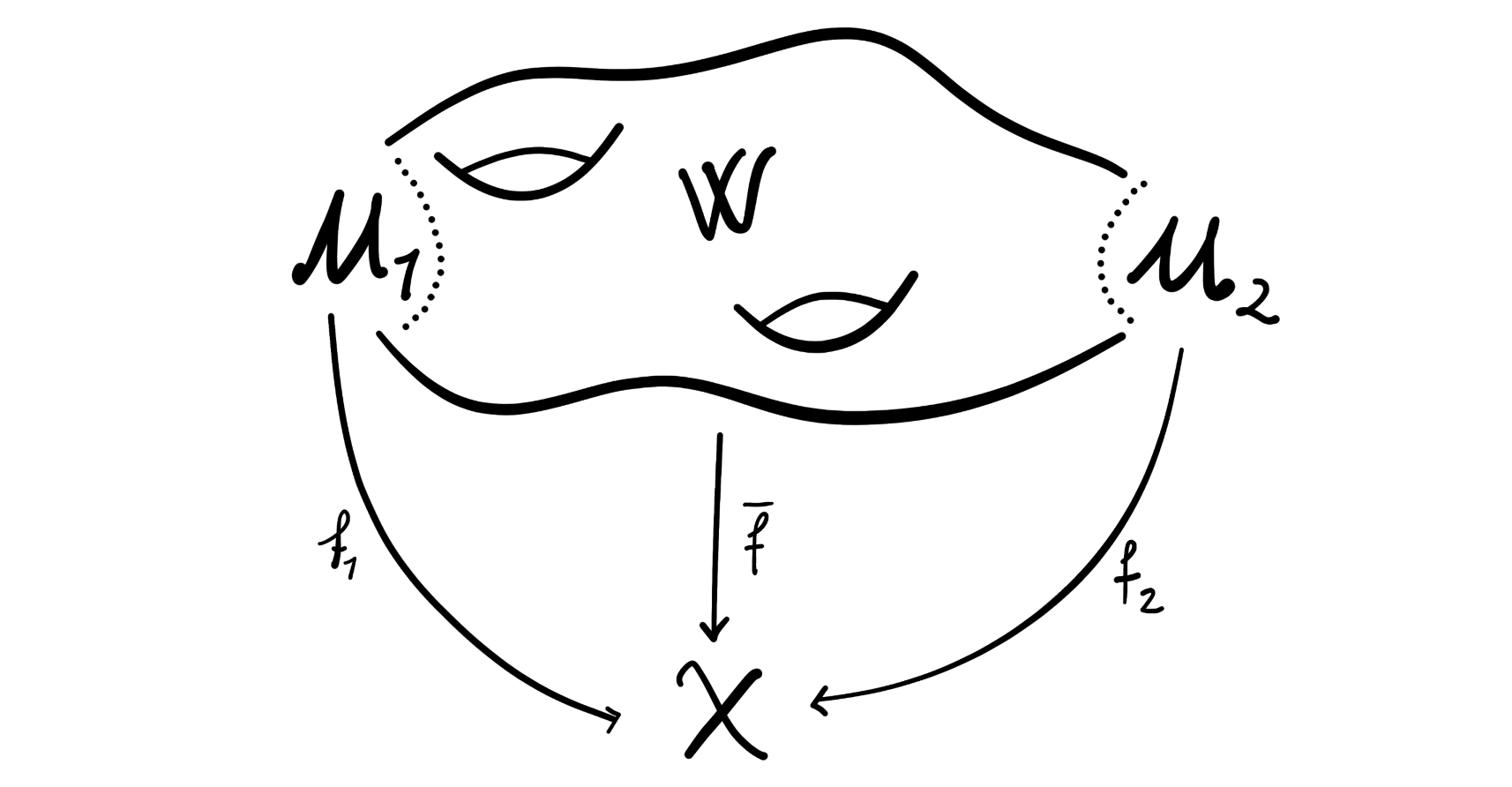
Johnson-Wilson theory
It has been some time since we studied at the correlation between formal group laws, which were certain power series that looked like Taylor expansion of multiplication on a Lie group, and complex oriented cohomology theories. In particular, we learned that these two completely separate notions had a common universal object. The universal formal group law over the Lazard ring was the same as the formal group law determined by the universal complex oriented cohomology theory — complex cobordism cohomology....