Stable homotopy theory

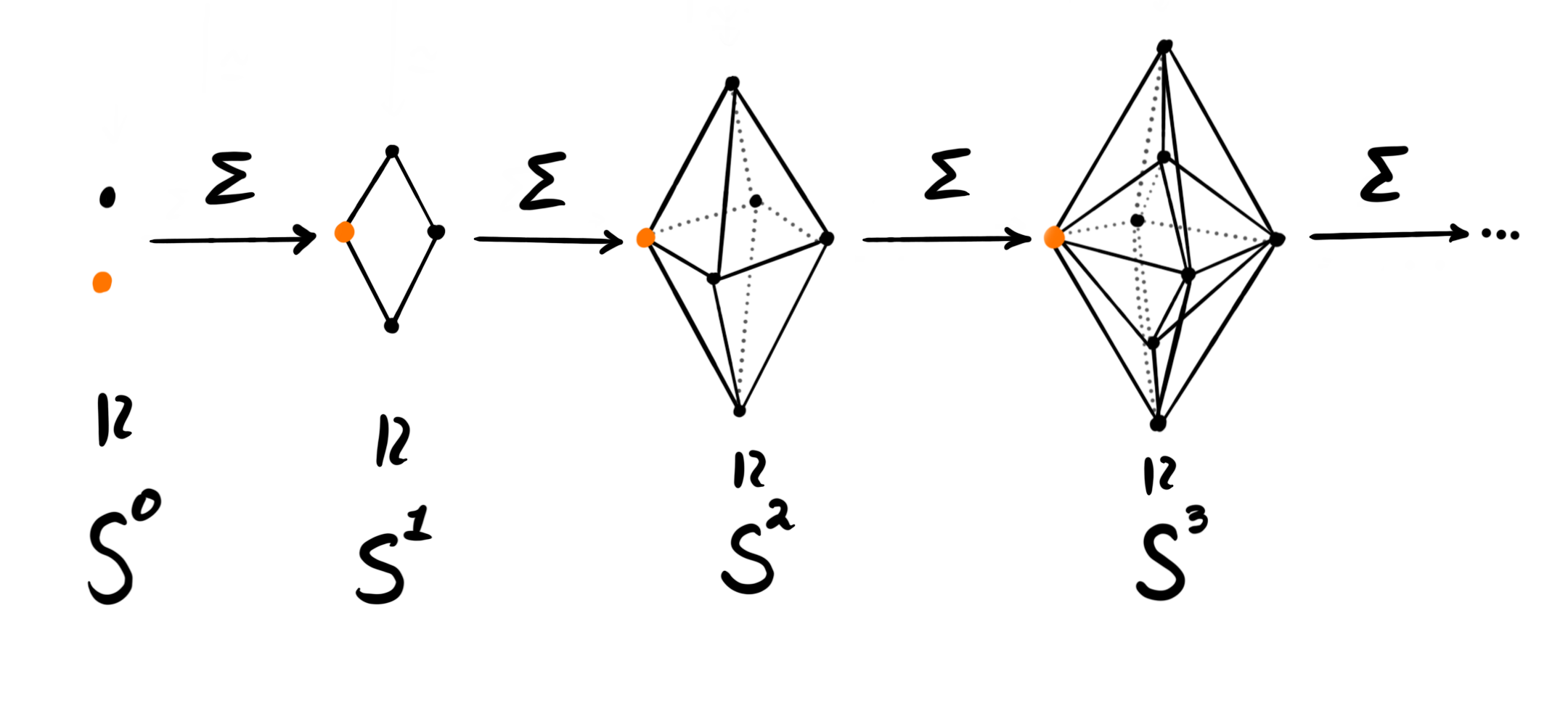
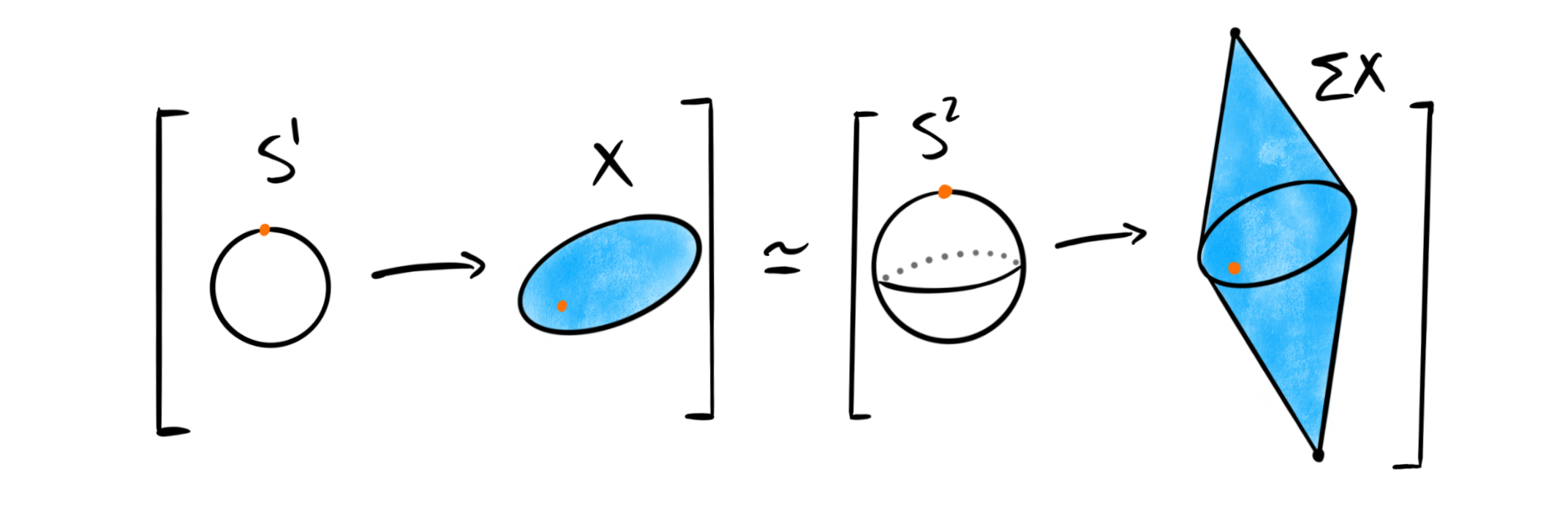
In the previous post we studied some “easy” cases of homotopy groups of spheres. We focused most on the group $\pi_3(S^2)$ and its computation from the Hopf fibration. All groups calculated last time were part of the so-called unstable range, meaning that they are not invariant under suspension. Due to the Freudenthal suspension theorem we know precicely the stable range for homotopy groups of spheres, and these are given by the stable homotopy groups....

A little while ago we discussed the definition of a tensor triangulated category, and in that post we mentioned an example that we didn’t explicitly define, namely the stable homotopy category. The goal for todays post is to fix this. There are many ways of defining it, and some are actually better than others. As the name suggests, the stable homotopy category is a homotopy category, which we have discussed before in the fibration series....

For the last few posts we have covered some theory surrounding cohomology theories, and today we want to do something else, namely again look at some homotopy theory. It’s been a long time since we have covered homotopy groups, but today we return once again. In particular I want to cover a theorem and its consequences — the Freudenthal suspension theorem. This is one of the central theorems in the homotopy theory of topological spaces, and is one of the more important theorems we left out from the fibration series....

Recently we have covered a lot of heavy topology and abstract mathematics, so today I thought we would cover something else — something maybe a bit easier to grasp. We will introduce the concept of formal group laws, and a bit on why they are interesting. Introduction and definition To not just spew out the definition straight away, we look at a situation where formal group laws arise very naturally. Let $G$ be a one-dimensional commutative Lie group (Think here of the real numbers $\mathbb{R}$ or the circle group $S^1$)....

Even though this blog is not centered around a specific topic, we have during the last year looked more frequently at certain topics than others, such as (co)homology theory, homotopy theory and category theory. We will continue this trend today as we will try to find a solid reason for a particular object to exist. These objects were briefly mentioned in the earlier post on tensor triangulated categories, namely spectra. These objects are hugely important to the field of algebraic topology, one reason being that they are intimately linked to cohomology....

For the last five years mathematics has been my passion, as well as my main focus in life. This passion for mathematics will hopefully not diminish, as I am now heading into four more years of studies and research through a PhD in mathematics at NTNU. I am joining a project, called Tensor triangulated geometry in Trondheim, so today I thought I would explore the definition of one of the main players in this theory, namely tensor triangulated categories....